以下认为 \(n,m\) 同阶。
首先,我们可以根据每次走的方向用一个二进制数来表示一条折线。这样显然有一个傻逼 DP,设 \(f_{i,S}\) 表示已经确定了前 \(i\) 条折线,其中第 \(i\) 条折线的状态为 \(S\) 的方案数,这样复杂度是 \(O(4^n \text{poly}(n))\) 的。
注意到这个转移的形式和轮廓线 DP 十分类似,于是我们可以使用同样的方式优化:先按照折线从左到右,再按照每条折线从上到下依次确定,那么上一条折线中比当前点往前的部分都不用考虑了。于是我们可以修改一下 DP 的定义,设 \(f_{i,j,k,S}\) 已经确定了前 \(i\) 条折线和第 \(i+1\) 条折线的前 \(j\) 个位置,第 \(i\) 条折线在当前层和当前位置距离为 \(k\)、后半部分为 \(S\) 的 \(j+1 \sim n\) 位,当前折线的前半部分为 \(S\) 的 \(1 \sim j\) 位,在这种情况下的方案数。其中 \(i,j\) 两位都可以滚掉,但总时间复杂度 \(O(2^n n^3)\),还是过不去。
上面做法的瓶颈在于,在抹掉上一条折线的前半部分时我们把它的位置信息也给抹掉了,这时候我们不得不多用一个状态 \(k\) 来确定它的位置。如果,我们能够在抹除上一条折线的前半部分的同时利用当前折线确定出位置,是不是就大功告成了?
顺着这个思路我们继续往下想。如果执意要完整记录下上一条折线的话,看起来并没有很好的解决方案。但是仔细想想,我们其实只关心上一条折线限制了当前折线的哪些位置,而对于一些不可能走到的位置,其实可以不记录那些状态。也就是说,我们把上一条折线右侧的区域,和这条折线未来可能走到的区域,取个交,对答案也没有影响。
从官方题解里贺来的图:
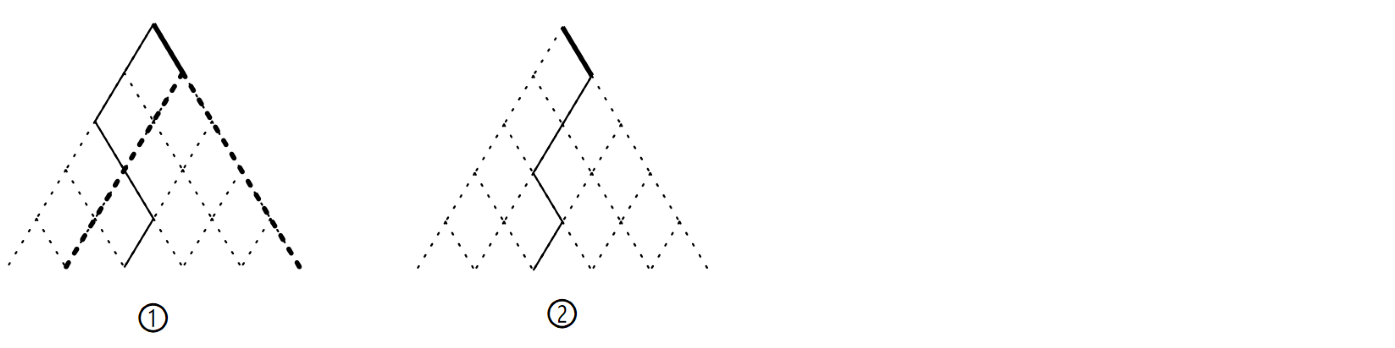
于是我们可以认为上一条折线是直接从当前位置出发的,而当前位置可以直接由 \(S\) 确定,这样就把 \(k\) 给扔掉了。
我们修改一下 DP 的定义:设 \(f_{i,j,S}\) 表示已经确定了前 \(i\) 条折线和第 \(i+1\) 条折线的前 \(j\) 个位置,满足如下条件的方案数:当前折线的前 \(j\) 个位置恰好为 \(S\) 的 \(1 \sim j\) 位,且在之后的过程中,当前折线不能走到折线 \(S\) 的左边。
考虑如何转移,我们设上一条折线对当前折线的限制为 \(P = (p_1,\cdots,p_{n-1})\),当前折线为 \(Q = (q_1,\cdots,q_k)\),显然 \(\forall i \in [1,k),p_i = q_i\)。转移有两种情况:
-
若 \(q_k = p_k\),那么不需要对 \(P\) 进行修改。
-
否则一定有 \(q_k = 1\) 且 \(p_k = 0\)。如果不存在 \(i > k\) 使得 \(p_i = 1\),那么我们将 \(p_k\) 修改为 \(1\)。否则,找到最小的这样的 \(i\),将 \(p_k\) 修改为 \(1\),将 \(p_i\) 修改为 \(0\) 即可。可以结合图片理解这个过程。
上述操作都可以利用二进制操作在 \(O(1)\) 时间内完成。\(i,j\) 两维都可以滚掉,总时间复杂度为 \(O(2^n n^2)\)。
code
/*
挥拂去蒙尘半生的晦暗
用这嶙峋双臂迎接 振翅吧 我的蝴蝶
最后一支 赤诚赞歌盘旋
潮起潮落翻覆昼夜 澎湃在生命刻度之前
此刻色彩挣脱谎言 献予你 赤红纸花遍野
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 20, mod = 1e9 + 7;
int n, m, k, t[N][N], f[2][1 << N];
void add(int &x, int y) { x += y; if (x >= mod) x -= mod; }
int main() {
ios :: sync_with_stdio(0);
cin >> n >> m >> k; --n;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
t[i][j] = -1;
for (int i = 1, a, b, c; i <= k; i++) {
cin >> a >> b >> c;
t[--a][--b] = c;
}
int o = 0;
f[o][0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
o ^= 1;
for (int S = 0; S < 1 << N; S++) f[o][S] = 0;
for (int S = 0; S < 1 << N; S++) if (f[o ^ 1][S]) {
int v = f[o ^ 1][S];
if (t[i][j] != 1) {
if (~S >> j & 1) add(f[o][S], v);
}
if (t[i][j] != 0) {
if (S >> j & 1) add(f[o][S], v);
else {
int T = S >> j;
if (T) T &= T - 1;
T = (T + 1) << j | (S & ((1 << j) - 1));
add(f[o][T], v);
}
}
}
}
}
int ans = 0;
for (int S = 0; S < 1 << N; S++) add(ans, f[o][S]);
cout << ans << endl;
return 0;
}
原文地址:http://www.cnblogs.com/came11ia/p/16817290.html
