假设检验

开篇语

假设检验，相信大伙儿或多或少都接触过，比如你的实验有两组（实验组、对照组）数据，你要分析一下它们之间的差异，那么假设检验是怎么也绕不过去的步骤。反正你不想做，你导师也会要求你做的，你导师不要求，你投稿时，那些reviewers也会要求你做的……

既然躲不开绕不去，那我们也不用怕它，小编今天就来跟大伙儿好好理一理，假设检验到底是啥东东，应该怎么玩！

基本概念与套路

什么是假设检验呢？从字面上看，肯定得先有个假设对吧，然后我们就来检验这个假设是不是成立，听上去很简单嘛！说得专业一点其实也不难理解，就是根据得到的数据，对我们预先设定的假设进行统计学检验，最后判断结果是否有统计学意义。

基本套路一般是：

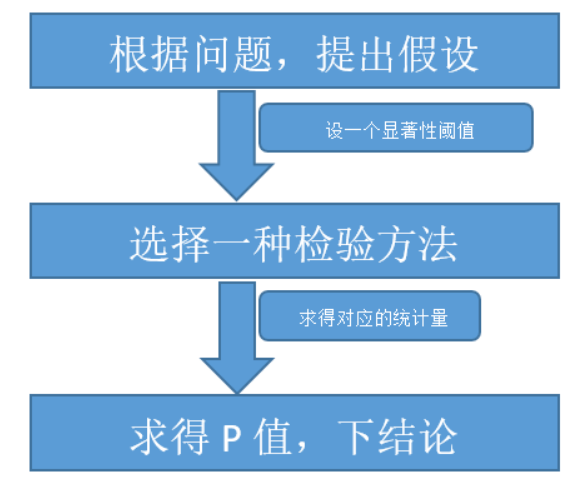
套路清楚后，我们现在来拆解套路：

根据问题 提出假设 

什么是“假设（hypothesis）”呢？牛津词典中有这样的解释：A supposition or proposed explanation made on the basis of limited evidence as a starting point for further investigation。看着有点晕是不是？我们来个通俗的理解就是，当我们没有足够的证据（即先验知识）来说明一个问题时，我们可以先给出一个假定的说明。这个预先给出的假定说明，我们通常称为原假设或者零假设，与之对应的，我们还可以提出一个对立假设，又称为备择假设。

举个例子。当我们拿到一个硬币，想研究一下它的正反面是否均匀，我们可以先假设它是不均匀的，这个就是零假设；那么对应的，它正反面是均匀的，就是备择假设。

PS：一般来说（并不绝对），原假设就是需要我们收集证据来反对的假设，而备择假设就是需要收集证据来支持的假设。

扩展阅读

为啥有了零假设，我们还需要弄一个对应的备择假设呢？对备择假设的重要性，
90多年前，英国著名的统计学家哥色特（其笔名就是Student）曾举例解释过这个问题，
他的主要思想就是人们往往都倾向于选择相信概率比较大的事件。
比如一些来自于正态总体的数据，现想检验它们的均值是不是等于a0？
假设得到检验的概率值为0.0001，虽然这个值很小，但是你不能认为这批数据的均值不等于a0，为什么呢？
因为这时候你只有一个a0供你检验，概率值再小，也不能否认它发生的可能性。
而此时，如果你再有一个“备胎”（值为a1）让你去检验，最后检验的概率值为0.05，比前面的值大很多，
这时候你就会倾向于选择后面a1这个值，而认为原来的a0不真。
所以，我们需要有“比较”，多一个“备胎”，多一份选择！（此例子原型来源于《数理统计学简史》）。

“假设”通常有三种形式，以我们最熟悉的生物样本数据的差异分析来举例，当我们分析的是单个样本时，我们可以比较这个样本的数据与一个已知值的关系，是大于，小于，还是等于。

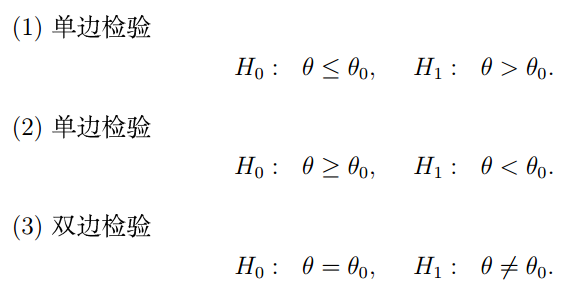
所谓单边检验，就是检验我们拿到的数据与一个已知值相比，是否大于等于它（或者小于等于它，你可以理解为，只需要判断数轴一侧的大小关系，所以叫单边检验），双边检验就是看两个值是否相等（你可以理解为，既不能大于，也不能小于，两边不等的情况都得排除，所以叫双边检验）。

当我们分析的是两个样本，考察它们之间是否存在差异，也有三种情况，就是样本1的值大于等于样本2，或者小于等于样本2，或者样本1与样本2相等。

扩展阅读

两个样本的假设的形式如下图（其中H₀为原假设，H₁为备择假设）：

再有一种情况就是分析多个样本之间的差异，这时候就无所谓大于小于这些单边检验了，只有全部相等（或不全相等）的情况。

扩展阅读

多个样本之间的情况如下图所示：

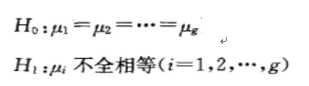
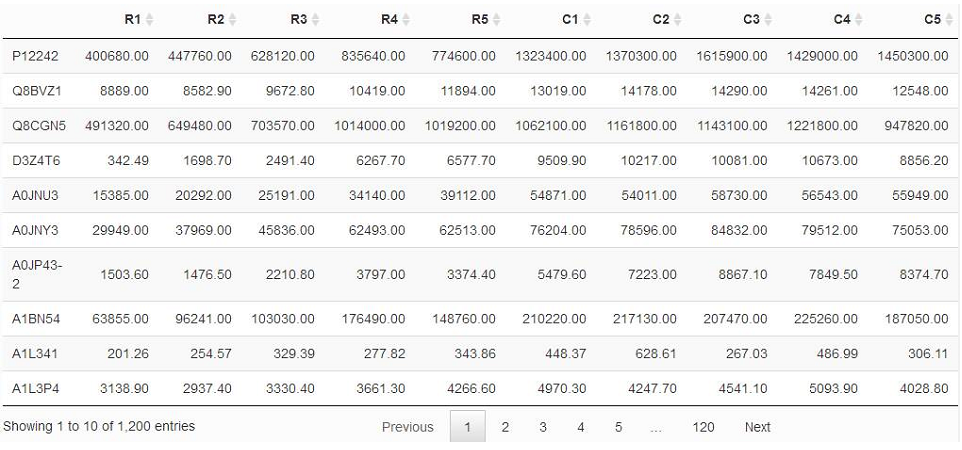
 如果上面的解释和公式你还是觉得有点晕，那么我们来举个例子，以蛋白质定量数据为例，分析两组数据之间是否存在差异，我们假设现在有两大组数据（R, C），每一组得到5次生物学重复数据。得到数据如下：

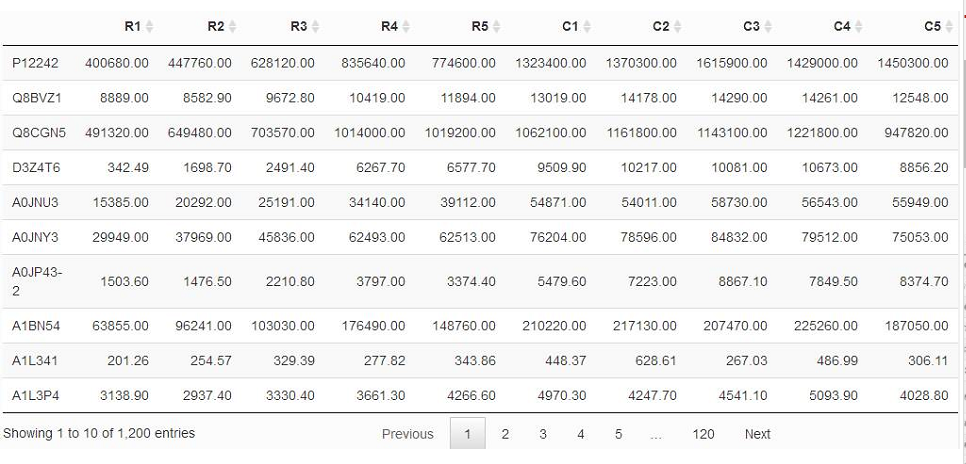
比如我们想看蛋白质P12242在R组和C组的平均表达量（分别设为μ₁，μ₂）是否一致，也就是说，要么相等，要么不等，大伙儿可以对照着看看上面提到的两个样本双边检验的说明。此时我们做原假设H₀，即该蛋白质在两组中表达量相等（μ₁=μ₂），那么备择假设就是H₁，即该蛋白质在两组中表达量不相等（有差异，即μ1≠μ2）。

假设给出来以后，我们一般会先选定一个显著性水平a，也就是一个判断的阈值，当统计分析出来的p值小于这个阈值时，说明是有统计显著性的，可以推翻原假设。通常可以设为0.05，严格一点可以设置为0.01，具体设多少要根据你的实验设计和目的，可以做一定的调整。

扩展阅读

为啥我们要设一个显著性水平a作为阈值呢？这就得说到假设检验中通常爱犯的两类错误（如下表）：第一类错误（又称I型错误）是，否定了真实的原假设，即“弃真”，对应上面的例子就是，原假设是蛋白质P12242在两组中的表达量平均值是没有差异的，本来它是成立的，结果被你否定了，你认为有差异，这就产生了错误；第二类错误（又称II型错误）是，接受了错误的原假设，即“取伪”。怎么控制第一类犯错误的概率呢？就是我们通常说的设定一个显著性水平α，第二类犯错误的概率通常标记为β。

 可以告诉你的是，在给定样本的情况下，减少犯其中一类错误的概率，就会导致增加犯另一类错误的概率。所以若想同时减少犯两类错误概率，就需要增加样本的容量。这就是为什么我们在分析差异表达的时候，通常都对样本量有一定的要求，否则你就算是做了这些假设检验，结果也比较难有说服力。当然，增加样本容量就会增加实验成本，所以通常建议在能力容许的范围内，尽可能的多增加一些样本量。

选择一种检验方法

好，我们继续说“蛋白质P12242在两组中的表达量平均值是没有差异”这个故事。上面的部分我们已经把假设列好了，原假设就是它们没差异，备择假设是它们有差异。接下来，我们就得开始检验这个假设了。

检验假设当然是需要有检验方法的！检验方法当然是不止一种的！针对这个例子，我们列出几种常用的假设检验的方法。做假设检验的一般思路就是，根据某种分布，求出数据对应的统计量，以此来判断该值是否落入拒绝域中（即拒绝原假设的取值范围），从而也可以得到对应的概率值P（以前可通过查表得到，现在通过计算机可以快速计算）。所以，接下来我们就以各种分布为主线，跟大伙儿聊聊假设检验的常见思路，详细的方法介绍我们会在下一篇推文中进行全面的总结。

 正态分布和t分布（T检验）

正态分布，大伙儿从小就听说过吧！它也许是最常见，最重要的一种分布形式了。它虽不是著名数学家Gauss第一个提出的，但是他将之应用于天文学研究，使其广为人知，所以正态分布通常又称为高斯分布。

扩展阅读

正态分布的概率密度函数表达式为：

 其中m和s为两个常数，m表征数据的均值，s表征数据的标准差。此时可称随机变量X服从参数为m, s的正态分布，记作X~N(m, s²)。

（其中红线表示的是均值为-2，方差为1的正态分布曲线，蓝线表示的是均值为2，方差为4的正态分布曲线。

从中可以看出，方差越小，图像越“瘦高”，方差越大，图形越“矮胖”。）

 t分布是由英国著名统计学家哥色特发表，其笔名是“Student”，所以该分布又称为“Student t分布”。该分布的公布，标志着小样本统计推断的开始。

扩展阅读

其随机变量T的表达式为：

其中X~N(0, 1)，Y~C-²-(n)，且X，Y相互独立，其自由度为n，记作T~t(n)。

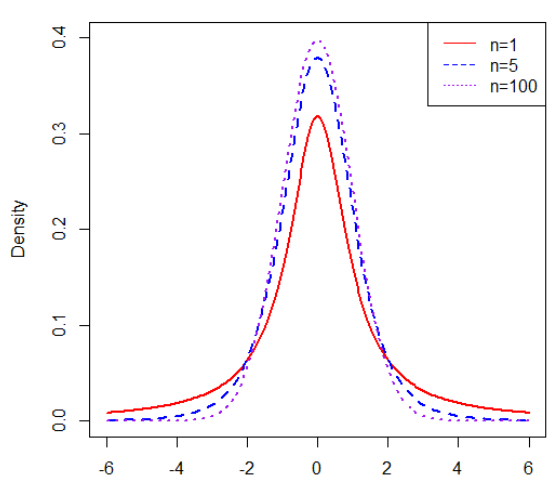
 （红线、蓝线、紫线分别是自由度为1、5、100的T分布曲线。大家也许发现了，T分布与正态分布曲线看上去是不是很像，这里主要是因为T分布是为了小样本的数据分布，当自由度n趋于无穷大时，T分布曲线就越接近标准正态分布曲线。）

下面我们继续使用上面蛋白质定量数据的例子，来说明一下t.test函数的使用：

现在我们想检验蛋白质P12242在R组和C组的平均表达量（分别设为μ₁，μ₂）是否一致。我们已经设定好了原假设H₀，即该蛋白质在两组中表达量相等（μ1=μ2），那么备择假设就是H₁，即该蛋白质在两组中表达量不相等（有差异，即μ1≠μ2）。

然后我们选择一种检验方法，这里我们假设两组数据满足正态分布，所以我们选择用T检验来评估它们是否有差异（如何判断数据是否满足某种分布，这个问题后面我们会再讲）。

读入数据，

 在R语言中可以直接使用t.test函数可进行T检验，函数原型为：

 其中x, y是我们样本数据构成的向量，alternative表示备择假设的形式，“two.sided”表示双边检验（H1: μ₁≠μ₂）， “less”表示单边检验（H1:μ₁<μ₂），“greater”表示单边检验（H1:μ₁>μ₂），paired表示样本是否是配对的，var.equal表示两总体方差是否相等。

在这个例子中，t.test函数调用如下：

最后得到P值等于0.0001212，小于0.05，可以支持我们拒绝原假设，即我们认为蛋白质P12242在R组和C组的平均表达量不相等。

通过以上的假设检验，我们就可以挑选出表达差异的基因/蛋白质，进行后续生物学意义上的注释、分类、聚类、相互作用关系分析等。

扩展阅读

怎么判断两样本是否配对？一般出现以下情况中的任意一种，就认为是配对的：

• 配对的两个受试对象分别接受两种不同的处理；

• 同一受试对象接受两种不同的处理；

• 同一受试对象处理前后的结果进行比较（即自身配对）；

• 同一对象的两个部位给予不同的处理。

F分布（方差分析）

另一种常用来评估各数据组均数之间差异的方法叫方差分析，用这种方法，可以评估所有观测数据之间的波动程度，不同组之间的波动，以及组内数据的波动。

与方差分析相关的是F分布，由1924年英国统计学家R.A.Fisher提出，所以用Fisher的第一个字母F来命名。假设有两个独立的随机变量，这两个变量都分别符合卡方分布，它们相除以后的比率，我们就用F分布来描述。

扩展阅读

假设样本X~c²(n)，Y~c²(m)，且X和Y相互独立，则称随机变量F：

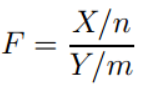
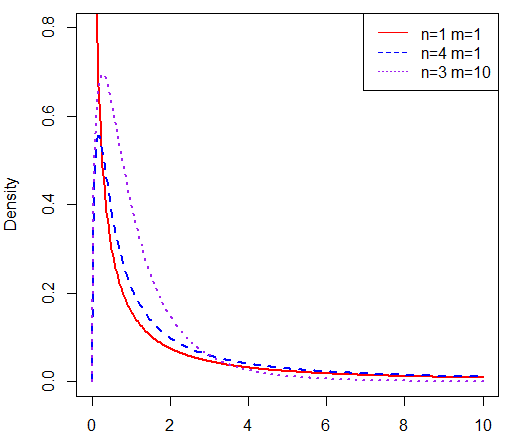
 服从自由度为（n, m）的F分布，记作F~F（n, m）。使用R语言画出F分布曲线及R代码如下：

在R语言中，我们通常使用aov函数进行计算分析：

其中formula是方差分析的公式，data就是我们的数据集，其是数据框的形式。

formula中各符号表达的含义可以参考《R语言实战》一书，在使用的过程中要注意不要搞混了：

 我们来举个例子说说aov的使用，比如分析小白鼠接种了3中不同菌型的伤寒杆菌后，平均存活的天数有无显著差异？原始数据如下：

 代码实现：

 从结果中得p值为0.0012，小于0.05，即认为3组小鼠的平均存活天数有显著性差异。

扩展阅读

在进行aov函数分析之前，我们一般要对数据进行正态性检验和方差齐性检验，在R语言中常用到的函数分别为shapiro.test和bartlett.test。只有满足要求的数据，我们才能进行该方法的计算。对于不满足要求的数据，我们可以采用秩和检验的方法，比如KW秩和检验（使用kruskal.test函数）或者Friedman秩和检验（使用friedman.test函数）。它们的详细使用我们计划在下一篇推文中详细介绍。

卡方分布（卡方检验）

上面我们讲了针对数据差异分析的检验方法，接下来跟大伙儿聊聊如何检验数据是否符合某种分布，包括对列联表的小样本量数据的检验。

话说，如果有n个相互独立的随机变量，它们都服从标准正态分布，那么这n个随机变量的平方和可以构成一个新的随机变量，这个新的随机变量分布的规律称为卡方分布。是不是很厉害的样子？

扩展阅读

卡方分布的形式是这样的，我们假设样本X_i~N(0,1)，其中i=1,2,3…n，则随机变量Y：

则称Y~c²(n)，即Y服从自由度为n的卡方分布

R语言代码如下:

 图形如下（其中红线、蓝线、紫线分别是自由度为1、4、10的卡方分布曲线），

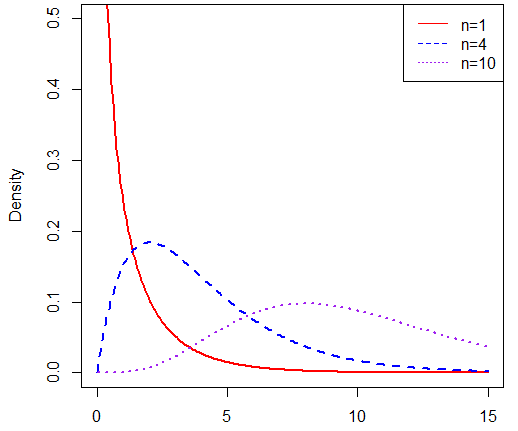
如果以卡方分布为理论依据进行假设检验，这种检验方法我们称为卡方检验。

卡方检验主要用在两个方面：

a. 检验数据是否服从某种分布，比如卡方分布、均匀分布、泊松分布、正态分布等

b. 检验列联表数据。

Tips
啥叫列联表呢？其实就是交互分类表。交互分类是同时依据两个或多个变量的值，
将所研究的个案分类。交互分类的目的是将两个或者多个变量分组，
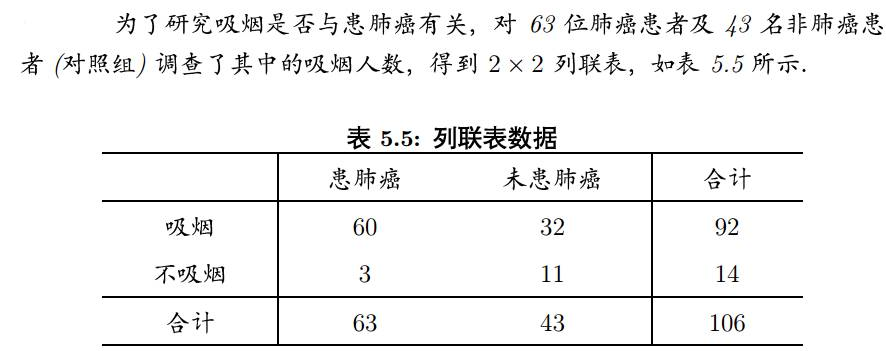
然后比较各组的分布状况，以寻找变量间的关系。比如下面这个列联表，
就是依据是否吸烟与是否患肺癌进行分类，然后可以通过比较这些数值，寻找吸烟与患肺癌之间是否相关。

R语言中使用chisq.test函数进行计算：

 其中x, y为数据向量，correct表示是否进行连续性修正；p表示原假设落在某区间的理论概率，默认的是均匀分布；rescale.p=FASLE的意思是要求输入的p之和要等于1；simulate.p.value表示是否使用仿真的方法计算p值，B是指仿真的次数。

检验数据是否服从某种分布  

说了这么多，到底我怎么检验我们的数据是符合什么分布呢？接下来我们就来举个例子。

我们都知道，不管是中考、高考、还是某类大型考试，某部门一般都爱要求老师给学生打的成绩要服从正态分布，那么现在假设我们得到了这样一批学生的成绩，我们想来检验下这批学生的成绩是否服从正态分布呢？

代码如下：

从结果中可得p值等于0.06161，大于0.05，可认为此次老师批阅试卷的成绩服从正态分布。

在检验数据服从某种分布时，我们还可以使用Kolmogorov-Smirnov检验，也是可以用于检验各种常见的分布，其函数是ks.test。比如还是上面那个例子，其代码实现如下：

 得到的p值为0.2162，也是大于0.05，得的结论与上面一致，即此次的成绩符合正态分布。

检验列联表数据  

列联表是啥刚才已经解释过了，我们常见的就是2×2的列联表形式，还是吸烟与肺癌的例子：

 

 

 代码实现如下：

所得的p值为0.004855，小于0.05，可以认为吸烟与患癌病有关。

检验列联表数据时，我们还常会用到Fisher检验，该检验是建立在超几何分布的基础上，当样本量比较小时（这里有个经验值，频数小于4），一般建议使用该检验方法。

Tips
1）超几何分布：是统计学上一种离散概率分布，描述的是，从有限个物件中抽出n个物件，
成功抽出指定类型的物件的次数（不归还）。比如，在产品质量的抽检中（抽出来的不放回去），
如果N件产品中有M件次品，抽检n件时所得次品数X，就服从超几何分布。
2）频数：也称“次数”，对整个数据按某种标准分组，然后统计出各个组内含个体的个数。

比如上面例子中，有一个频数为3（不吸烟患肺癌这一组），所以这里建议使用Fisher检验，其代码实现如下：

 

 

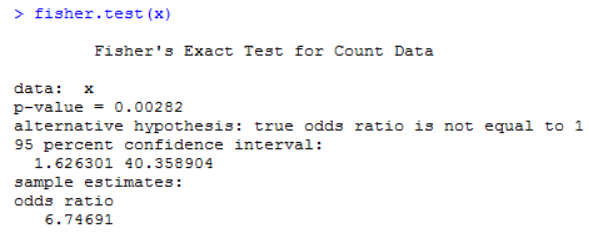
 所得的p值为0.00282，小于0.05，所得结论与上面一致。且这里还给出了优势比（odds ratio）的值，该值大于1，其含义是吸烟越多，患肺癌的可能性就越大。

求得P值，下结论

其实在第2部分我们举例说明的时候就已经做了这一步。在这里，我们想着重说明一下的是：

a.     在我们下结论的时候，其实是用了一个大家广泛接受的原则：在一次试验中，小概率事件基本上不会发生。若它正好发生了，那么我们就有理由怀疑原假设的准确性；

b.    对于显著性水平a的大小（比如0.01, 0.05, 0.1之类），这个大小没有一个绝对的定值，只要你能说出一些合理的理由，你完全可以调整这个值的界限。若是对这些约定俗成的值感兴趣的，可以去看看那些老前辈的文章（比如《Statistical methods for research workers》）；

c.     从前面描述，我们都可以看出，我们所下结论时都是根据p值而来，所以，在描述结论的时候一定不能下绝对的结论，比如“认为3组小鼠的平均存活天数一定（或肯定）有差异”，这种结论是不严谨的；

d.    我们所说的“具有显著性差异”，这个表现不出具体差异的大小，只能说明它们存在差异，所以，这也是我们在分析数据时，经常会看到大家不仅关注p值，还同时关注倍数（fold change）变化的原因，这种可视化表现形式尤其以火山图最为著名。

原文地址：http://www.cnblogs.com/rongdie/p/16787651.html