前言
上一章:[01] 离散型随机变量基础
概念
连续型随机变量取值范围是无限不可数集合(如全体实数)。
连续型随机变量的定义是:设X为随机变量,存在非负函数f(x)使得:
$F(x)=\int_{-\infty}^{x}f(t)\mathrm{d}t$
其中\(f(x)\)为概率密度。
性质
-
\(f(x)\ge 0;\)(曲线位于x轴上方)
-
\(\int_{-\infty}^{+\infty}f(x)\mathrm{d}x=1.\) (与x轴之间的面积为1)
这两条都挺直观的,就不过多解释。如果不理解就去看上一篇离散型变量吧。
常见分布
均匀分布(矩形分布)
均匀分布是对称概率分布,在相同长度间隔的分布概率是等可能的。
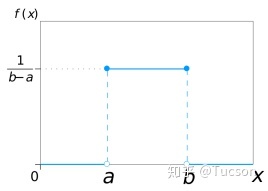
\(f(x)=\left\{\begin{matrix} \frac{1}{b-a} \\\ 0 \end{matrix}\right.\begin{matrix} a<x<b \\ \mathrm{others} \end{matrix}\)
指数分布
指数分布可以看作是几何分布的连续版本。
某些元件或设备的寿命服从指数分布.例如无线电元件的寿命 、电力设备的寿命、动物的寿命等都服从指数分布。
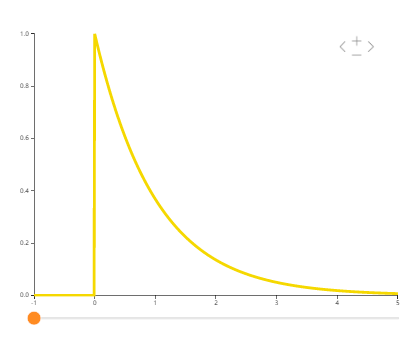
\(f(x)=\left\{\begin{matrix} \lambda e^{-\lambda x} ,\\ 0, \end{matrix}\right. \begin{matrix} x>0, \\ x \le0. \end{matrix}\)
正态分布(高斯分布)
$N(\mu, \sigma^2)$
是钟形曲线。科学中常用正态分布来模拟许多小效应的叠加。比方说,我们知道人的身高是许多微小的基因和环境效应的叠加。因此可以用正态分布来表示人的身高。
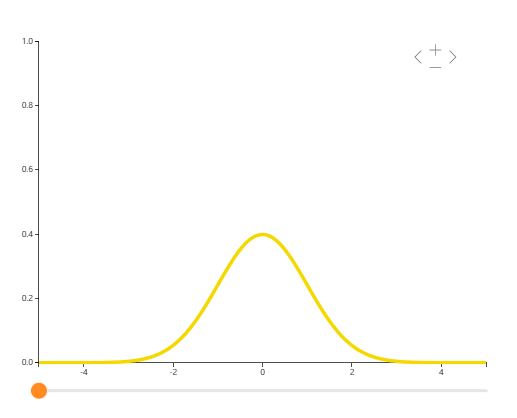
这个概率密度函数比较复杂(非初等函数):
\(f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma ^2} }\)
特征
- \(x=\mu\)是对称轴;
- \(x\)轴是渐近线;
- 最大值为\(\frac{1}{\sqrt{2\pi}\sigma}\);
- 不改变\(\mu\)的情况下,\(\sigma\)越大,图像越矮胖;反之则图像更瘦高。
计算方法
- 利用MatLab计算;
- 转化为标准正态分布查表计算
标准正态分布
当正态分布中的\(\mu = 0, \sigma = 1\)时,这样的章台分布称为标准正态分布。此时记为:\(N(0,1)\)。
其概率密度表示为:
\(\varphi(x)=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{x^{2}}{2}}\)
更新中…
原文地址:http://www.cnblogs.com/canisidea/p/16829527.html
