【CFgym102870J】Junction of Orz Pandas（思维，容斥）

暴力做法就不会做……

考虑容斥，用所有数 \(\leq a_i\) 的方案减去所有数 \(<a_i\) 的方案得到最大值为 \(a_i\) 的方案，\(b_i\) 同理容斥，时间复杂度 \(O(2^{n+m}nm)\)。

直接在容斥上优化是没有前途的，考虑换一种思路。

发现我们交换两行或交换两列并不影响答案，那我们不妨将 \(a_i\) 和 \(b_i\) 从小到大排序。

我们先取出 \(v\) 为所有 \(a_i\) 和 \(b_i\) 的最小值，假设有 \(x\) 个 \(a_i\) 等于 \(v\)，\(y\) 个 \(b_i\) 等于 \(v\)：

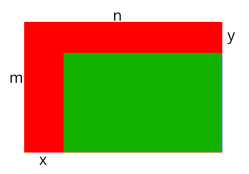
显然红色部分都需要满足 \(\leq v\)，那么无论红色部分怎么取值都对第 \(x+1\sim n\) 列、第 \(y+1\sim m\) 行是否满足限制没有任何影响，于是我们可以对红色部分单独处理，对绿色部分继续递归处理。那么我们就能将原来的矩形分成很多个 L 字形，每个 L 字形分别统计方案数，最后再乘起来即可。

接下来是单独对每个 L 字形统计方案数，这个时候就能用一开始讲的容斥做法了：

观察到将常数和只跟 \(i\) 有关的部分提到前面去后，后面剩下来的是个 \(\sum_{j=0}^{y}\binom{y}{j}A^{y-j}B^j\) 的形式，为二项式展开，可以快速幂 \(O(\log y)\) 求。

所以求一次 L 字形是 \(O(x\log y)\) 的。总时间复杂度 \(O(n\log n)\)。

#include<bits/stdc++.h>

#define N 100010
#define ll long long

using namespace std;

namespace modular
{
	const int mod=998244353;
	inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
	inline int dec(int x,int y){return x-y<0?x-y+mod:x-y;}
	inline int mul(int x,int y){return 1ll*x*y%mod;}
	inline void Add(int &x,int y){x=x+y>=mod?x+y-mod:x+y;}
	inline void Mul(int &x,int y){x=1ll*x*y%mod;}
}using namespace modular;

inline int poww(int a,ll b)
{
	int ans=1;
	while(b)
	{
		if(b&1) ans=mul(ans,a);
		a=mul(a,a);
		b>>=1;
	}
	return ans;
}

inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<1)+(x<<3)+(ch^'0');
		ch=getchar();
	}
	return x*f;
}

int n,m,t,a[N],b[N];
int fac[N],ifac[N];

int C(int n,int m)
{
	return mul(mul(fac[n],ifac[m]),ifac[n-m]);
}

int main()
{
	n=read(),m=read(),t=max(n,m);
	fac[0]=1;
	for(int i=1;i<=t;i++) fac[i]=mul(fac[i-1],i);
	ifac[t]=poww(fac[t],mod-2);
	for(int i=t;i>=1;i--) ifac[i-1]=mul(ifac[i],i);
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=m;i++) b[i]=read();
	sort(a+1,a+n+1),reverse(a+1,a+n+1);
	sort(b+1,b+m+1),reverse(b+1,b+m+1);
	int ans=1;
	while(n&&m)
	{
		int v=min(a[n],b[m]);
		int x=0,y=0;
		while(x<n&&a[n-x]==v) x++;
		while(y<m&&b[m-y]==v) y++;
		v%=mod;
		int sum=0;
		const int div=mul(dec(v,1),poww(v,mod-2));
		for(int i=0;i<=x;i++)
		{
			int tmp=mul((i&1)?mod-1:1,mul(C(x,i),poww(div,1ll*m*i)));
			Mul(tmp,poww(dec(1,poww(div,n-i)),y));
			Add(sum,tmp);
		}
		Mul(ans,mul(sum,poww(v,1ll*m*x+1ll*n*y-1ll*x*y)));
		n-=x,m-=y;
	}
	if(n||m)
	{
		puts("0");
		return 0;
	}
	printf("%d\n",ans);
	return 0;
}

原文地址：http://www.cnblogs.com/ez-lcw/p/16837415.html