
(没穿红色的可莉……)
题目描述
给定一张 \(n\) 个点 \(m\) 条边的连通图,每条边有权值 \(w\) ,定义从 \(u_1\) 到 \(u_x\) 经过边 \(e_1,e_2,…,e_k\) 的路径长度为:
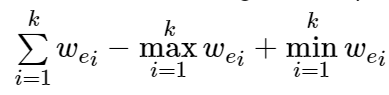
请分别对于每个点 \(i∈[2,n]\) 求出点 \(1\) 到 \(i\) 的长度最小的路径。
输入格式
第一行两个数,代表 \(n,m\)。
接下来 \(m\) 行每行三个数 \(u,v,w\),代表一条连接 \(u,v\) 长度为 \(w\) 的边。
输出格式
对于每个 \(i\) 输出点 \(1\) 到 \(i\) 长度最小的路径的长度,用空格分隔。
样例 #1
样例输入 #1
5 4
5 3 4
2 1 1
3 2 2
2 4 2
样例输出 #1
1 2 2 4
提示
【样例解释】
- 当 \(i=2\) 时经过路径 \(1→2\)
- 当 \(i=3\) 时经过路径 \(1→2→3\)
- 当 \(i=4\) 时经过路径 \(1→2→4\)
- 当 \(i=5\) 时经过路径 \(1→3→5\)
【数据范围】
对于 \(30\%\) 的数据,\(1≤n≤1000\)
对于另 \(30\%\)的数据,\(m=n-1\)
对于 \(100\%\) 的数据,\(1≤n,m≤1×10^5;0≤w_i≤10^9\)
解析
对于题干中的路径长度定义我们可以这样理解:将最长边的边权变为0,最短边的边权变成两倍,相当于有两次操作(对于一条路径有且仅能有这两个操作),我们可以用分层图的思想(一共建4层),首先每层都由x向y连z的无向边,第一层向第二层连边权为0的边,再向第三层连2倍边权的边,第二层向第四层连2倍边权,第三层向第四层连0边(巧妙的建图方法)对于一种操作向上连边,这样保证第四层都是有两次操作的,其实2.3层相当于是一个过渡,最后的答案就是第一层和第四层的d[]取min,那么答案为什么是这个呢?因为1->i可能直接相连,那么答案就是在第一层中找(只有一条边不可能还进行两次操作),答案统计过程包含了对该种情况的特判。求d[]用最短路算法就行了,我这里用的spfa。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10;
int n, m, tot, head[N], to[N << 3], nxt[N << 3], w[N << 3], d[N];
bool vis[N];
void add(int x, int y, int z) {
nxt[++ tot] = head[x]; head[x] = tot; to[tot] = y; w[tot] = z;
}
void spfa() {
memset(d, 0x3f, sizeof d);
queue<int> q;
d[1] = 0, q.push(1); vis[1] = 1;
while (!q.empty()) {
int u = q.front(); q.pop(); vis[u] = 0;
for (int i = head[u]; i; i = nxt[i]) {
int v = to[i];
if (d[v] > d[u] + w[i]) {
d[v] = d[u] + w[i];
if (!vis[v]) {
vis[v] = 1;
q.push(v);
}
}
}
}
}
signed main() {
cin >> n >> m;
for (int i = 1; i <= m; i ++) {
int u, v, w; cin >> u >> v >> w;
for (int i = 0; i <= 3; i ++) {
add(u + i * n, v + i * n, w);
add(v + i * n, u + i * n, w);
}
add(u, v + n, 0), add(v, u + n, 0);
add(u, v + 2 * n, 2 * w), add(v, u + 2 * n, 2 * w);
add(u + n, v + 3 * n, 2 * w), add(v + n, u + 3 * n, 2 * w);
add(u + 2 * n, v + 3 * n, 0), add(v + 2 * n, u + 3 * n, 0);
}
spfa();
for (int i = 2; i <= n; i ++) {
int ans = min(d[i], d[i + 3 * n]);
printf("%lld ", ans);
}
return 0;
}

原文地址:http://www.cnblogs.com/YHxo/p/16792745.html
