1. 向量的概念与运算
1. 向量
- 向量:既有大小又有方向的量叫做向量,或称矢量
- 标量:只有大小(可用一个数值表示)
- 向量的几何表示:有向线段 \(\overrightarrow{P_1P_2}\)或者\(\vec{a}\):以\(P_1\)为起点,为\(P_2\)终点的有向线段
- 向量相关概念
- 模:向量的大小,记作 \(|\overrightarrow{P_1P_2}|\)或者\(|\vec{a}|\)
- 单位向量:与向量\(\vec{a}\)具有相同方向的单位向量,叫做\(\vec{a}\)的单位向量,记为 \(\vec{a}^0 = \frac{\vec{a}}{|\vec{a}|}\)
- 零向量:模为零的向量 \(\vec{0}\)或者\(\mathbf{0}\)
- 相等向量:如果两个向量的模相等且方向相同,那么叫做相等向量,记作\(\vec{a}=\vec{b}\)
- 反向量:两个模相等,方向相反的向量叫做互为反向量,\(\vec{a}\)的反向量记作\(-\vec{a}\),\(\overrightarrow{AB} = -\overrightarrow{BA}\)
- 平行向量:平行于同一直线的一组向量叫做共线向量;零向量与任何共线的向量组共线
- 共面向量:平行于同一平面的一组向量叫做共面向量;零向量与任何共面的向量组共面
2. 向量的加法
-
三角形法则:设向量\(\vec{a},\vec{b}\),以空间任意一点\(O\)为起始点连接做向量\(\overrightarrow{OA} = \vec{a},\overrightarrow{AB}=\vec{b}\)得到折线\(OAB\);从折线的端点\(O\)到另一个端点\(B\)的向量\(\overrightarrow{OB}=\vec{c}\),叫做两向量\(\vec{a},\vec{b}\)的 和,记作 \(\vec{c}=\vec{a}+\vec{b}\)
-
平行四边形法则:如果两个向量\(\overrightarrow{OA},\overrightarrow{OB}\)为邻边组成平行四边形\(OACB\),那么对角向量\(\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}\)
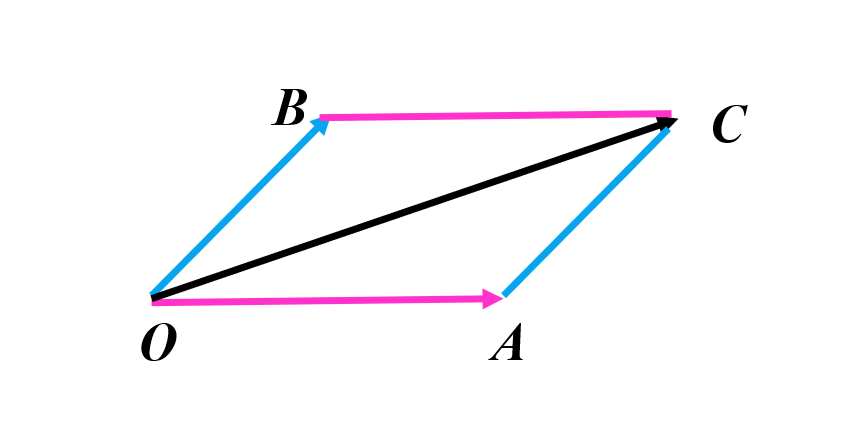
-
运算规律
- 交换律:\(\vec{a}+\vec{b} = \vec{b}+\vec{a}\)
- 结合律:\((\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})\)
- 零元:\(\vec{a}+\vec{0}=\vec{a}\)
- 逆元:\(\vec{a} + (-\vec{a}) = \vec{0}\)
3. 向量的减法
- 减法:当\(\vec{b}+\vec{c}=\vec{a}\),我们把\(\vec{c}\)叫做\(\vec{a}\)和\(\vec{b}\)的差,记作\(\vec{c}=\vec{a}-\vec{b}\)
- 减法后的向量方向终点指向被减向量的端点:\(\overrightarrow{BA} = \overrightarrow{OA} – \overrightarrow{OB}\)
4. 向量的数乘
- 数乘:由向量的加法可知,\(n\)个向量\(\vec{a}\)相加方向为\(\vec{a}\),大小为\(|n|\times|\vec{a}|\)的向量\(n\vec{a}\)
- 模:\(|\lambda\vec{a}| = |\lambda||\vec{a}|\)
- 方向:当\(\lambda>0\),与\(\vec{a}\)方向相同;当\(\lambda>0\),与\(\vec{a}\)方向相反
- \(0\vec{a} = \vec{0}\)
- 运算规律
- 一乘不变性:\(1\cdot\vec{a}=\vec{a}\)
- 结合律:\(\lambda(\mu\vec{a}) = \mu(\lambda\vec{a}) = (\lambda\mu)\vec{a}\)
- 第一分配律:\((\lambda+\mu)\vec{a} = \lambda\vec{a}+\mu\vec{a}\)
- 第二分配律:\(\lambda(\vec{a}+\vec{b}) = \lambda\vec{a}+\lambda\vec{b}\)
- 平行:设\(\vec{a}\ne\vec{0}\),那么\(\vec{b}\)平行于\(\vec{a}\)的充分必要条件是:存在唯一的实数\(\lambda\),使得\(\vec{b}=\lambda\vec{a}\)
2. 向量的线性组合与向量分解
1. 向量的线性组合
- 线性运算:向量的加法和向量的数乘统称为向量的线性运算
- 线性组合:由向量 \(\vec{a_1}, \dots, \vec{a_n}\) 与实数\(\lambda_1, \dots, \lambda_n\)所组成的向量 \(\vec{a} = \lambda_1\vec{a_1} + \dots + \lambda_n\vec{a_n}\)叫做向量的 线性组合
- 共线:如果 \(\vec{e}\ne\mathbf{0}\),那么向量 \(\vec{r}\)与\(\vec{e}\)共线的充要条件是\(\vec{r}\)可以由\(\vec{e}\)线性表出,即\(\vec{r} = x\vec{e}\),并且系数\(x\)被唯一确定
- 共面:如果 \(\vec{e_1},\vec{e_2}\ne\mathbf{0}\),那么向量 \(\vec{r}\)与\(\vec{e_1},\vec{e_2}\)共面的充要条件是\(\vec{r}\)可以由\(\vec{e_1},\vec{e_2}\)线性表出,即\(\vec{r} = x\vec{e_1}+y\vec{e_2}\),并且系数\(x,y\)被唯一确定,其中\(\vec{e_1},\vec{e_2}\)被称为平面上的 基底
- 向量空间的基底:如果\(\vec{e_1},\vec{e_2},\vec{e_3}\)不共面,那么空间中任意向量\(\vec{r}\)都可以由\(\vec{e_1},\vec{e_2},\vec{e_3}\)线性表出,即写为\(\vec{r} = x\vec{e_1}+y\vec{e_2}+z\vec{e_3}\),\(x,y,z\)被唯一确定;其中\(\vec{e_1},\vec{e_2},\vec{e_3}\)被称为向量空间的基底
2. 向量的线性关系
- 线性相关:对于\(n\)个向量 \(\vec{a_1}, \dots, \vec{a_n}\), 如果存在不全为0的\(n\)个实数\(\lambda_1, \dots, \lambda_n\)使得 \(\lambda_1\vec{a_1} + \dots + \lambda_n\vec{a_n} = \mathbf{0}\),那么这\(n\)个向量 线性相关,不是线性相关的向量叫做 线性无关
- 对于一个向量\(\vec{a}\),当\(\vec{a}=\mathbf{0}\)时,\(\vec{a}\)线性相关
- 当\(n\ge 2\),向量 \(\vec{a_1}, \dots, \vec{a_n}\) 线性相关的充要条件时其中一个向量是其他向量的线性组合
- 如果一组向量中的一部分向量线性相关,那么这一组向量就线性相关
- 一组向量如果含有 零向量 ,那么这组向量就线性相关
3. 标架与坐标
1. 标架
- 标架:空间中一定点\(O\),连同三个不共面的有序向量\(\vec{e_1},\vec{e_2},\vec{e_3}\)的全体叫做空间中的一个标架,记作\(\{O;\vec{e_1},\vec{e_2},\vec{e_3}\}\)
- 笛卡尔标架:如果\(\vec{e_1},\vec{e_2},\vec{e_3}\)都是 单位向量,那么\(\{O;\vec{e_1},\vec{e_2},\vec{e_3}\}\)被称为笛卡尔标架
- 笛卡尔直角标架:\(\vec{e_1},\vec{e_2},\vec{e_3}\)两两垂直的笛卡尔标架叫做笛卡尔直角标架,或简称直角标架
- 仿射标架:一般情况下的标架
- 标架的顺序:对应手指顺序是 拇指、食指、中指
- 右旋标架(一般采用)
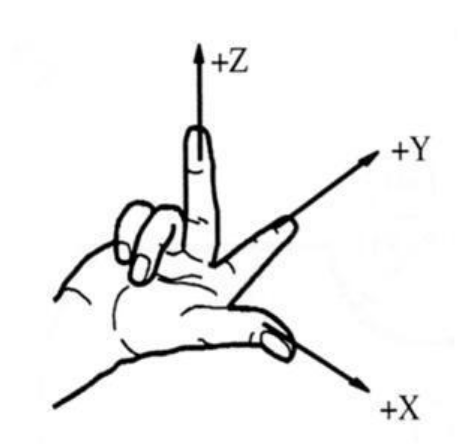
- 左旋标架

- 右旋标架(一般采用)
2. 坐标
- 坐标:空间中任意向量\(\vec{r}\)都可以由标架的\(\vec{e_1},\vec{e_2},\vec{e_3}\)线性表出,即写为\(\vec{r} = x\vec{e_1}+y\vec{e_2}+z\vec{e_3}\),其中\(x,y,z\)就是向量\(\vec{r}\)关于标架\(\{O;\vec{e_1},\vec{e_2},\vec{e_3}\}\)的 坐标,记作\(\vec{r}\{x,y,z\}\)或者\(\{x,y,z\}\)
- 向径:对于标架\(\{O;\vec{e_1},\vec{e_2},\vec{e_3}\}\)中的任意点\(P\),向量\(\overrightarrow{OP}\)叫做点\(P\)的向径
- 坐标系:当空间取定标架\(\{O;\vec{e_1},\vec{e_2},\vec{e_3}\}\)以后,向量空间中的\(\vec{r}\)和一个有序三元组\(\{x,y,z\}\)一一对应,这种一一对应的关系被称为空间向量的一个 坐标系,点\(O\)被称为坐标原点
-
直角坐标系:我们约定用\(\{O;\vec{i},\vec{j},\vec{k}\}\)表示直角坐标系,其中\(\vec{i},\vec{j},\vec{k}\)都是单位向量
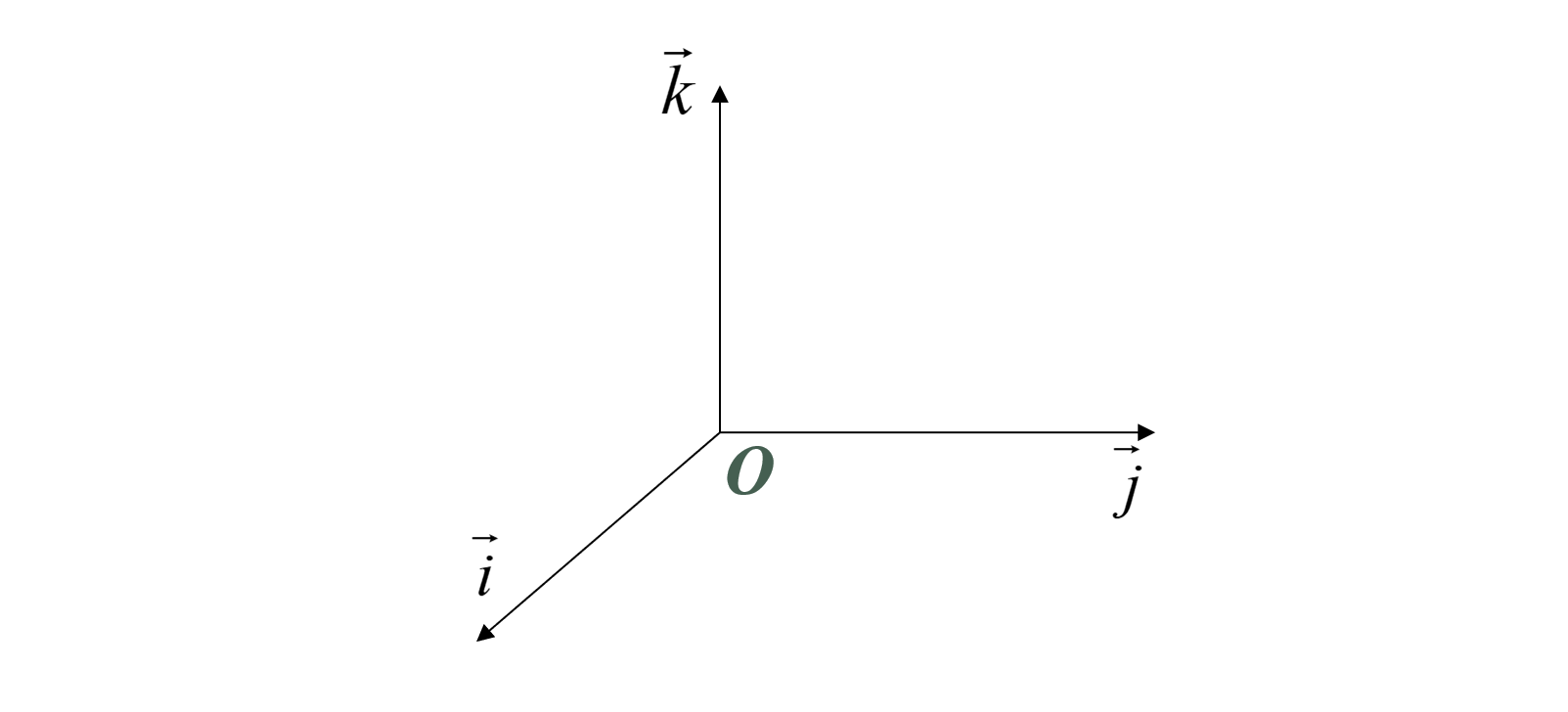
-
卦限:三维空间中的坐标系把空间分为8个 卦限
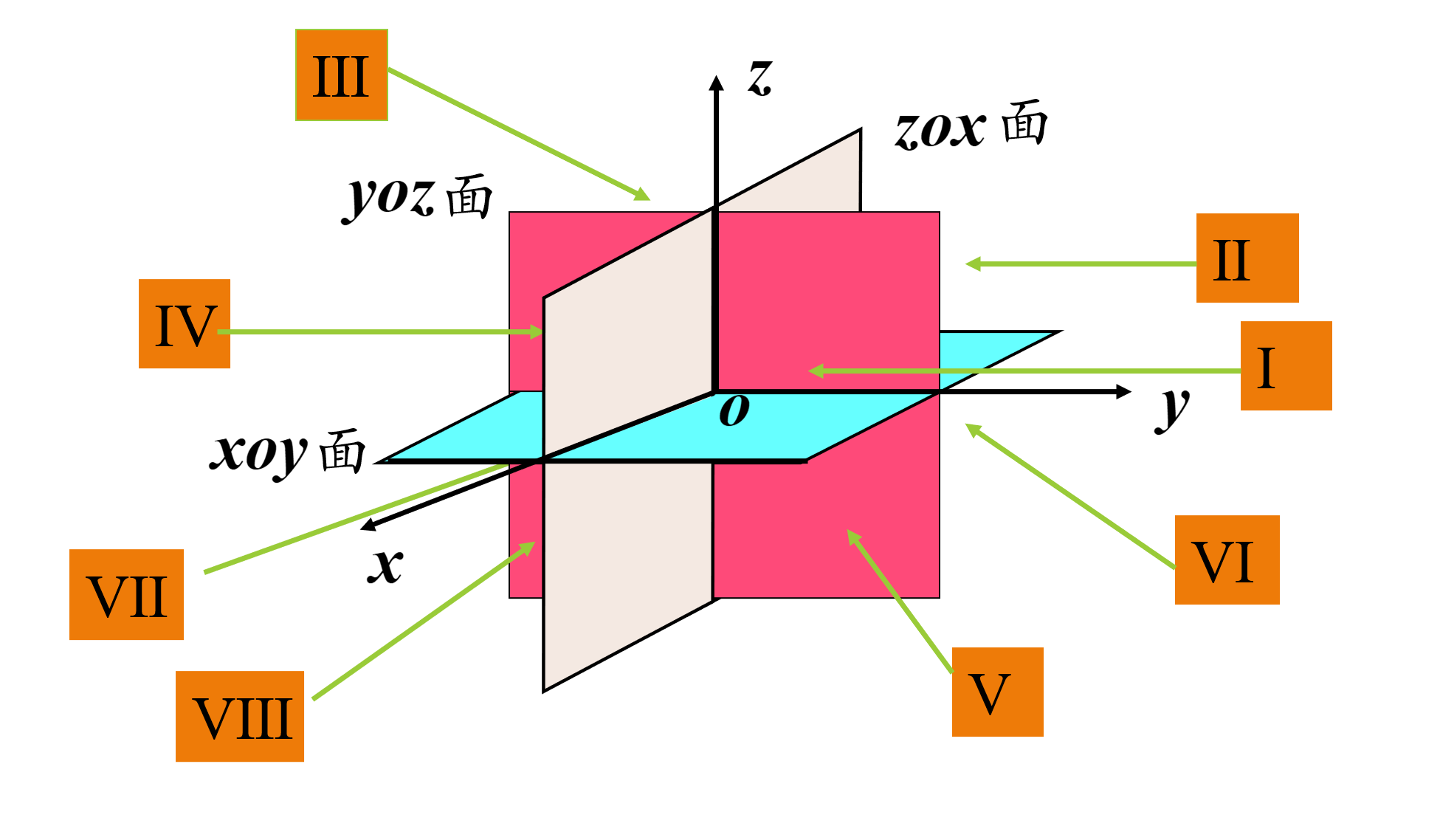
坐标\卦限 \(\mathrm{I}\) \(\mathrm{II}\) \(\mathrm{III}\) \(\mathrm{IV}\) \(\mathrm{V}\) \(\mathrm{VI}\) \(\mathrm{VII}\) \(\mathrm{VIII}\) x + – – + + – – + y + + – – + + – – z + + + + – – – –
-
- 向量的坐标运算
- 用向量的始点和终点的坐标表示向量的坐标:向量的坐标等于其终点的坐标减去其始点的坐标
- 用向量的坐标进行向量的线性运算
- 两向量和的坐标等于两向量对应的坐标的和
- 数乘向量的坐标等于这个数与向量的对应坐标的积
- 坐标表达式
- 向量的模的坐标表达式:\(|\vec{a}| = \sqrt{x^2+y^2+z^2}\)
- 两点之间的距离公式:\(d = \sqrt{(x_2 – x_1)^2+(y_2 – y_1)^2+(z_2 – z_1)^2}\)
- 共线:已知两非零向量\(\vec{a}\{x_1,y_1,z_1\},\vec{b}\{x_2,y_2,z_2\}\),则\(\vec{a},\vec{b}\)共线的充要条件是\(\frac{x_1}{x_2}=\frac{y_1}{y_2} = \frac{z_1}{z_2}\)
- 共面: 已知三个非零向量\(\vec{a}\{x_1,y_1,z_1\},\vec{b}\{x_2,y_2,z_2\},\vec{c}\{x_3,y_3,z_3\}\),则\(\vec{a},\vec{b},\vec{c}\)共面的充要条件是
\[\begin{vmatrix} x_1&y_1&z_1\\ x_2&y_2&z_2\\ x_3&y_3&z_3 \end{vmatrix}=0 \]
- 垂直:已知两非零向量\(\vec{a}\{x_1,y_1,z_1\},\vec{b}\{x_2,y_2,z_2\}\),则\(\vec{a},\vec{b}\)共线的充要条件是\(x_1x_2+y_1y_2+z_1z_2=0\)
- 线段的定比分点坐标
- 设\(A(x_1,y_1,z_1),B(x_2,y_2,z_2)\)为已知的两点,那么分有向线段\(AB\)成定比\(\lambda\)的分点的\(M\)的坐标是
\[x=\frac{x_1+\lambda x_2}{1+\lambda},y=\frac{y_1+\lambda y_2}{1+\lambda},z=\frac{z_1+\lambda z_2}{1+\lambda}, \]
- 设\(A(x_1,y_1,z_1),B(x_2,y_2,z_2)\)为已知的两点,那么分有向线段\(AB\)成定比\(\lambda\)的分点的\(M\)的坐标是
4. 投影
1. 空间一点在轴上的射影
- 射影:设已知空间的一点\(A\)与一轴\(l\),通过\(A\)做垂直于轴\(l\)的平面\(\alpha\),称该平面与轴\(l\)的交点\(A^{‘}\)叫做点\(A\)在轴\(l\)上的 射影
- 射影向量:设向量\(\overrightarrow{AB}\)的始点\(A\)与终点\(B\)在轴\(l\)上的射影分别是\(A^{‘},B^{‘}\),那么向量\(\overrightarrow{A^{‘}B^{‘}}\)叫做向量\(\overrightarrow{AB}\)在轴\(l\)上的 射影向量,记作射影向量\(_{l}\overrightarrow{AB}\)
2. 空间两向量的夹角
- 夹角:设\(\vec{a},\vec{b}\)是两个非零向量,从空间任意点\(O\),作\(\overrightarrow{OA}=\vec{a},\overrightarrow{OB}=\vec{b}\),由射线\(OA,OB\)构成的角度在\(0\)和\(\pi\)之间的角,叫做向量\(\vec{a},\vec{b}\)的夹角,记作\(\angle(\vec{a},\vec{b})\)
- 有向角:以向量\(\vec{a}\)扫过向量\(\vec{a},\vec{b}\)之间的夹角\(\angle(\vec{a},\vec{b})\)旋转到向量\(\vec{b}\),定义\(\vec{a}\)到\(\vec{b}\)的有向角如下
- 如果旋转是逆时针的,称有向角为\(\angle(\vec{a},\vec{b})\)
- 如果旋转是顺时针的,称有向角为\(-\angle(\vec{a},\vec{b})\)
3. 射影定理
- 向量\(\overrightarrow{AB}\)在轴\(l\)上的射影等于向量的模乘轴与该向量的夹角的余弦:\(_{l}\overrightarrow{AB}=|\overrightarrow{AB}|\cos(\angle(l,\overrightarrow{AB}))\)
- 射影的线性性质
- 加法:对于任意向量\(\vec{a},\vec{b}\)有\(_{l}(\vec{a}+\vec{b}) = _{l}\vec{a} + _{l}\vec{b}\)
- 数乘:对于任意向量\(\vec{a}\)和任意实数\(\lambda\),有\(_{l}\lambda\vec{a} = \lambda_{l}\vec{a}\)
5. 向量的积
1. 数量积
-
数量积:对于任意向量\(\vec{a},\vec{b}\),它们的 数量积 是它们的模和夹角\(\theta\) 余弦 的乘积(也叫内积,点积):\(\vec{a}\cdot\vec{b}=\vec{a}\vec{b}=|\vec{a}||\vec{b}|\cos\theta\)
-
数量积的性质
- 两向量的数量积等于其中一个向量的模和另一个向量在这向量的方向上的射影的乘积
- \(\vec{a}\cdot\vec{a}=|\vec{a}|^2 \ge 0\),当且仅当\(\vec{a}=\mathbf{0}\)时取等号
- \(\vec{a}\cdot\vec{b}=0 \Longleftrightarrow \vec{a}\perp\vec{b}\space(\vec{a},\vec{b}\ne \mathbf{0})\)
-
数量积运算规律
- 交换律:\(\vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{a}\)
- 分配律:\((\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}\)
- \((\lambda\vec{a})\cdot\vec{b} = \lambda(\vec{a}\cdot\vec{b}) = \vec{a}\cdot(\lambda\vec{b})\)
-
数量积的坐标表达式:设向量\(\vec{a}\{x_1,y_1,z_1\},\vec{b}\{x_2,y_2,z_2\}\),则\(\vec{a}\cdot\vec{b}=x_1x_2+y_1y_2+z_1z_2\)
-
方向余弦: 非零向量与三条坐标轴的正向的夹角称为 方向角,方向角的余弦,叫做向量的 方向余弦,约定非零向量\(\vec{r}\)与三个坐标轴的夹角作为方向角\(\alpha,\beta,\gamma\),方向余弦即为\((\cos\alpha,\cos\beta,\cos\gamma)\)
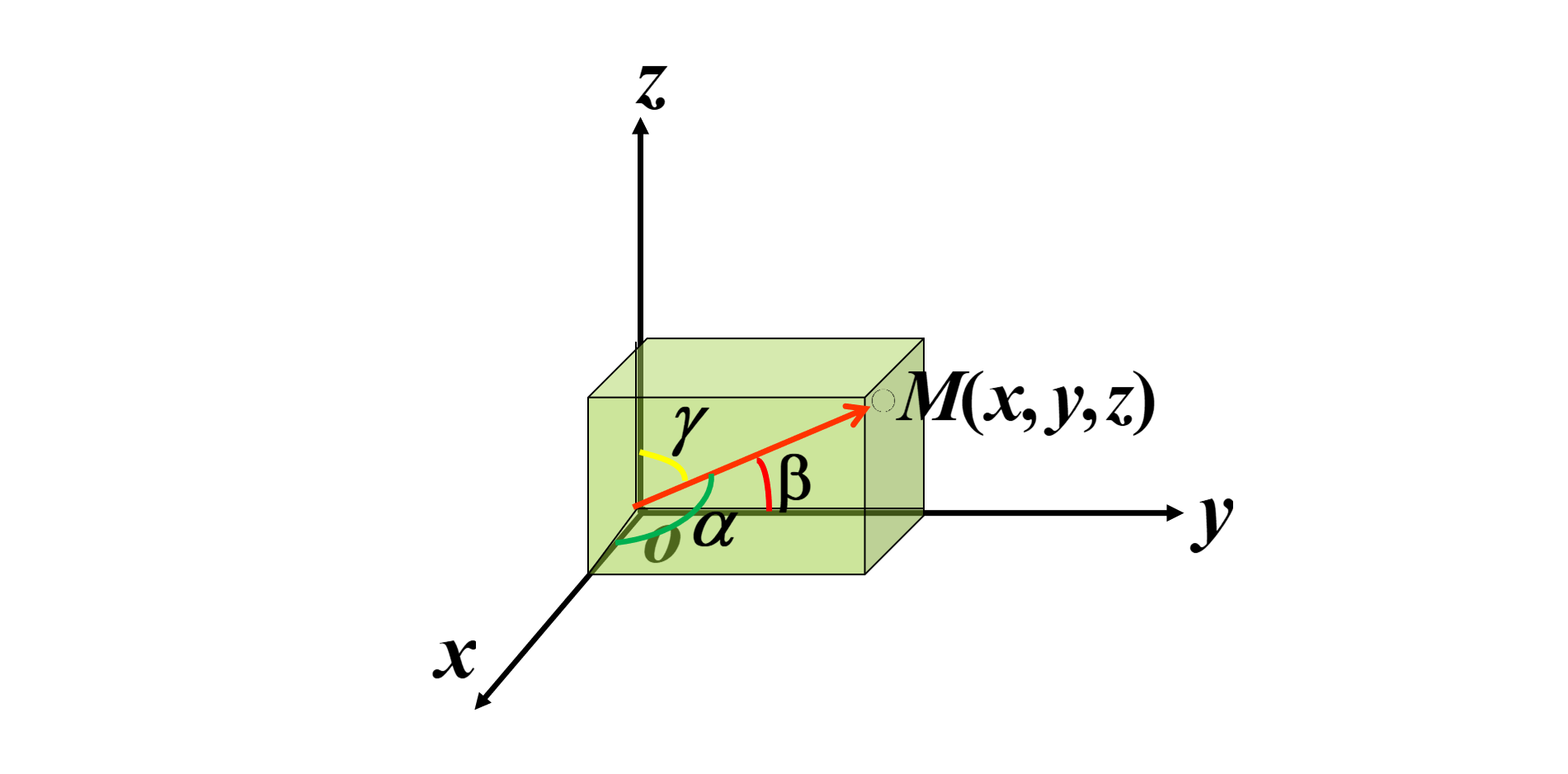
- 方向余弦的特征:\(\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1\)
- 方向余弦的特征:\(\vec{a}^0 = \frac{\vec{a}}{|\vec{a}|} = (\cos\alpha,\cos\beta,\cos\gamma)\)
2. 向量积
- 向量积:两向量\(\vec{a},\vec{b}\)的 向量积(也叫外积)是一个向量,记作\(\vec{a}\times\vec{b}\),它的模是\(|\vec{a}\times\vec{b}|=|\vec{a}||\vec{b}|\sin\angle(\vec{a},\vec{b})\),方向与\(\vec{a},\vec{b}\)垂直,并且按\(\vec{a},\vec{b},\vec{a}\times\vec{b}\)形成右手标架
- 共线:\(\vec{a},\vec{b}\)共线的充要条件是\(\vec{a}\times\vec{b}=\mathbf{0}\)
- 向量积运算规律
- 反交换律:\(\vec{a}\times\vec{b} = -\vec{b}\times\vec{a}\)
- 数因子结合律:\(\lambda(\vec{a}\times\vec{b}) = (\lambda\vec{a})\times\vec{b} = \vec{a}\times(\lambda\vec{b})\)
- 分配律:\(\vec{c}\times(\vec{a}+\vec{b}) = \vec{c}\times\vec{a}+\vec{c}\times\vec{b},(\vec{a}+\vec{b})\times\vec{c} = \vec{a}\times\vec{c}+\vec{b}\times\vec{c}\)
- 向量积的坐标表达式:设向量\(\vec{a}\{x_1,y_1,z_1\},\vec{b}\{x_2,y_2,z_2\}\),则
\[\vec{a}\times\vec{b}= \begin{vmatrix} \vec{i}&\vec{j}&\vec{k}\\ x_1 &y_1 &z_1\\ x_2 &y_2 &z_2 \end{vmatrix} \]
- 向量积的几何意义:\(\vec{a},\vec{b}\)向量积的大小等于由\(\vec{a},\vec{b}\)构成的平行四边形的 面积
3. 混合积
- 混合积:给定空间三个向量\(\vec{a},\vec{b},\vec{c}\),如果先作前两个向量\(\vec{a}\)与\(\vec{b}\)的向量积,再作所得向量\(\vec{a}\times\vec{b}\)与\(\vec{c}\)的数量积,最后得到的这个数叫做三向量的混合积,记作\((\vec{a}\times\vec{b})\cdot\vec{c}\)或者\((\vec{a}\vec{b}\vec{c})\)
- 混合积的几何意义:三个不共面的向量\(\vec{a},\vec{b},\vec{c}\)的混合积的绝对值等于以\(\vec{a},\vec{b},\vec{c}\)为棱的 平行六面体 的 体积
- 共面:空间三个向量\(\vec{a},\vec{b},\vec{c}\)共面的充要条件是\((\vec{a}\vec{b}\vec{c}) = 0\)
- 混合积的性质
- 轮换与对换:\((\vec{a}\vec{b}\vec{c}) = (\vec{b}\vec{c}\vec{a}) = (\vec{c}\vec{a}\vec{b}) = -(\vec{b}\vec{a}\vec{c}) = -(\vec{c}\vec{b}\vec{a}) = -(\vec{a}\vec{c}\vec{b})\)
- 混合积的坐标表达式
\[(\vec{a}\vec{b}\vec{c})= \begin{vmatrix} x_1 &y_1 &z_1\\ x_2 &y_2 &z_2\\ x_3 &y_3 &z_3 \end{vmatrix} \]
- 克莱姆法则:向量\(\vec{d}\)对于三个不共面的向量\(\vec{a},\vec{b},\vec{c}\)的分解式为\(\vec{d} = x\vec{a} + y\vec{b} + z\vec{c}\)
\[x = \frac{(\vec{d}\vec{b}\vec{c})}{(\vec{a}\vec{b}\vec{c})},y = \frac{(\vec{a}\vec{d}\vec{c})}{(\vec{a}\vec{b}\vec{c})},z = \frac{(\vec{a}\vec{b}\vec{d})}{(\vec{a}\vec{b}\vec{c})} \]
4. 双重向量积
- 双重向量积:给定空间三向量,先作其中两个向量的向量积,再作所得向量与第三个向量的向量积,那么最后的结果仍然是一个向量,叫做所给三向量的双重向量积:\(\vec{a}\times\vec{b}\times\vec{c}\)
- 双重向量积的计算:\((\vec{a}\times\vec{b})\times\vec{c} = (\vec{a}\cdot\vec{c})\vec{b} – (\vec{b}\cdot\vec{c})\vec{a}\)
- 拉格朗日恒等式
\[(\vec{a}\times\vec{b})\cdot(\vec{a^{‘}}\times\vec{b^{‘}})= \begin{vmatrix} \vec{a}\cdot\vec{a^{‘}} &\vec{a}\cdot\vec{b^{‘}}\\ \vec{b}\cdot\vec{a^{‘}} &\vec{b}\cdot\vec{b^{‘}} \end{vmatrix} \]
- 雅可比恒等式:\((\vec{a}\times\vec{b})\times\vec{c} + (\vec{b}\times\vec{c})\times\vec{a} + (\vec{c}\times\vec{a})\times\vec{b} = \mathbf{0}\)
原文地址:http://www.cnblogs.com/RadiumGalaxy/p/16869995.html
