前言:基本参照OIWIKI
数论
数论分块
参考博客henry_y
参考博客Miniqwq
常见形式:
画个双曲线图,在图上找到符合\(\lfloor\frac{k}{i}\rfloor\)的整点,具有单调性。
例子:
当\(n=7,k=7\)时:
发现可以将其分为块,每一块都是相等的数。
证明就不放上了,假定一个块的左端点为 \(l(l!=0)\),那么右端点为\(r=\lfloor\frac{k}{\lfloor\frac{k}{i}\rfloor}\rfloor\)
int l=1,r,n,k;
scanf("%d%d",&n,&k);
n=min(n,k);//这样写是因为n大于k的部分没有意义
while(l<=n)
{
r=min(k/(k/l),n);//r有可能会超过n
l=r+1;
}
应用
还是分块,然后用\(O(1)\)等差数列求出每个块的贡献即可。
例题
P3935 Calculating\(f(x)\)指的是x的因子个数,\(\sum\limits_{i=1}^nf(i)=\sum\limits_{i=1}^n\lfloor\frac{n}{i}\rfloor\)
欧拉函数
定义
欧拉函数,\(\varphi(n)\)表示\(\leq n\)与 \(n\)互质的数的个数。
性质
- 当\(n\)为质数时,\(\varphi(n)=n-1\)
- 欧拉函数为积性函数时,
\[\begin{equation*} \begin{aligned} & gcd(a,b) = 1 \\ &\Rightarrow \varphi(a*b)=\varphi(a)*\varphi(b) \end{aligned} \end{equation*} \]
- \(n=\sum\limits_{d|n}\varphi(d)\)
- 若\(n=p^k\),\(p\)为质数,则\(\varphi(n)=p^k-p^{k-1}\)
例:\(p=3,k=3\)时,与\(n\)不互质的数为\(3\thicksim27\)同时除以\(p\)为\(1\thicksim9\)即\(1\thicksim p^{k-1}\)

咱是真不愿意码了
欧拉定理
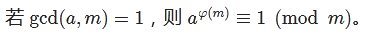
扩展欧拉定理
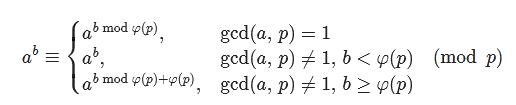
筛法
素数筛
埃氏筛法
把已知质数的所有倍数删掉(标记),再筛,接着筛,最后剩下的就是质数。
#include<bits/stdc++.h>
using namespace std;
const int N=100;
int vis[N+5];
vector<int> prime;
void Work()
{
for(int i=2;i<=N;i++)
{
if(!vis[i])
{
prime.push_back(i);
for(int j=2*i;j<=N;j+=i)
{
vis[j]=1;
}
}
}
}
int main()
{
Work();
for(int i=0;i<prime.size();i++)
{
cout<<prime[i]<<"\n";
}
return 0;
}
oiwiki有好多奇怪的写法优化,时间紧迫,不深究
线性筛
线性筛法的核心是:\(n\) 只会被最小质因子筛掉,复杂度 \(O(n)\)
例如 在埃氏筛中 \(6\) 会被 \(2\) 和 \(3\) 都筛一遍,增加了复杂度。
代码中两种情况的解释:
当 \(i \mod prime_j==0\) 时,\(prime_j\) 一定是 \(i\) 的最小质因子,因此 \(prime_j\) 一定是 \(prime_j * i\) 的最小质因子。
当 \(i \mod prime_j != 0\) 时,\(prime_j\) 一定小于 \(i\) 的最小质因子,因此\(prime_j\) 一定是 \(prime_j * i\) 的最小质因子。
懂了表达不出来,宝宝有苦说不出。
啊,我们的目的是在保证\(prime_j*i\)只会被最小的质因数\(prime_j\)所筛掉,手段就是利用线性筛去满足“上面两句中‘因此’前面的条件”。
#include<bits/stdc++.h>
using namespace std;
const int N=100;
int prime[N];
int tp;
bool vis[N];
void Work()
{
for(int i=2;i<=N;i++)
{
if(!vis[i])
prime[++tp]=i;
for(int j=1;prime[j]*i<=N;j++)
{
vis[prime[j]*i]=true;
if(i%prime[j]==0)//该操作保证了prime_j是i的最小质因子
break;
}
}
}
int main()
{
Work();
for(int i=1;i<=tp;i++)
{
cout<<prime[i]<<"\n";
}
return 0;
}
咕咕~还有好多线性筛求函数没写。
GCD
鸽
EXGCD
鸽
中国剩余定理(CRT)
人生建议,不要在学模板的时候仅看一个博客。
可以得到以下式子:
由此可得:
\(ans=(70*1+21*1+15*2)\mod (3*5*7)=16\)
真的谢了,不想写公式了,看别人的博客吧。
EXCRT
鸽~
BSGS
乘法逆元
求乘法逆元有四种:
前两种适合单次查询,后两种适合连续查询
①费马小定理的应用
限制:\(a \perp p\) 且 \(p \in prime\)
②EXgcd
限制:\(a \perp p\)
③O(n)线性
设 \(p=k*i+r\)
则
④O(n)阶乘求逆
原文地址:http://www.cnblogs.com/Estar-Mailyn/p/16735120.html
