摆放棋子
给定一个 $n \times m$ 的国际象棋棋盘(即一个 $n \times m$ 的方格矩阵)。
我们知道传统国际象棋中,主教(象)的行走规则是只能斜走,格数不限,但不可转向。
现在,我们对主教进行了修改,不妨称加强后的主教为大主教。
大主教仍然只能斜走,格数不限,但是当其走到棋盘边缘的方格时,它可以发生反射并继续移动,注意,如果没有走到棋盘边缘,则不能自行改变移动方向。
更具体地说,当它到达棋盘边(但并非角)上的方格时,它可以将移动方向改变 $90$ 度并继续移动,当它到达棋盘角上的方格时,它可以将移动方向改变 $180$ 度并继续移动。

请你计算,棋盘中共有多少种不同的移动轨迹。
输入格式
共一行,包含两个整数 $n,m$。
输出格式
一个整数,表示棋盘中移动轨迹的数量。
数据范围
前 $6$ 个测试点满足 $2 \leq n,m \leq 4$。
所有测试点满足 $2 \leq n,m \leq {10}^{6}$。
输入样例1:
3 4
输出样例1:
2
输入样例2:
3 3
输出样例2:
3
解题思路
由于证明比较麻烦,这里直接说结论,详细证明见参考资料中的链接。
每一条路径都是一个循环路径,并且一定会碰到边界的某个格子,同时每一个边界的格子最多只会出现在某个路径当中。意味着边界的每一个格子只会唯一对应某条路径,不会出现多条路径包含同一个边界格子这种情况。一条路径可能会对应边上多个格子,反过来边界上某些格子可能会对应同一条路径。因此如果想要统计路径的数量,就可以统计四个边界的格子中一共对应几条不同的路径,这个就可以用并查集来实现。
枚举矩形上下两条横边的格子(这里统一规定矩形的长大于等于宽),把属于同一个路径上的格子进行合并。

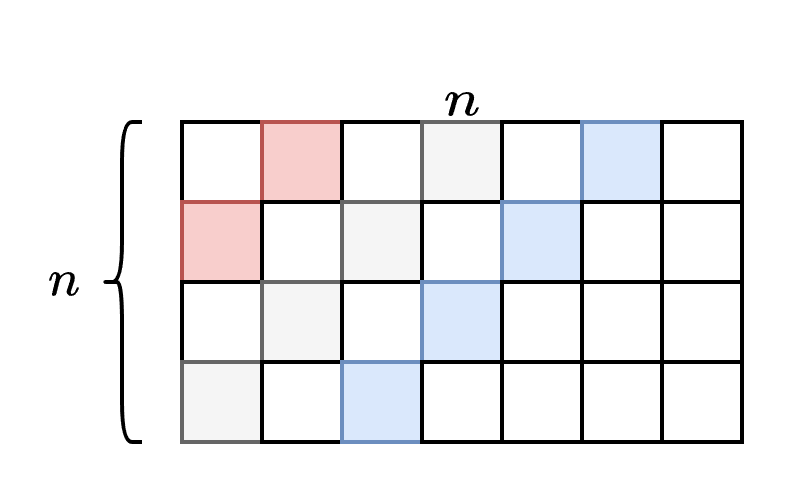
比如上图中的红色格子,从红色格子往两个方向走分别可以走到蓝色格子的位置,这时就将红色格子与两个蓝色格子进行合并,某条路径会经过这个三个格子。
矩形的左右两条竖边就不用枚举了,因为可以发现从竖边的格子往两个方向走一定会走到两条横边的某个格子并进行合并,而在枚举到这两个横边的格子时就已经将这个竖边的格子合并了,因此不用再枚举竖边的格子了。
在枚举横边的格子时需要分成两种情况。当枚举从格子向左的方向走时,要以矩形的宽$n$为分界,当格子的纵坐标$i \leq n$时会走到左边的竖边,当$i < n$时会走到下边的横边。
当枚举从格子向右的方向走时,要以从右边数第$n$个格子(即从左边数第$m-n+1$个格子)为分界,当格子的纵坐标$i \geq m – n + 1$时会走到右边的竖边,当$i > n$时会走到下边的横边。

最后由于格子是一个二维坐标,因此还需要对四条边上的格子进行标号,这里从左上角开始进行顺时针标号。
AC代码如下:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int N = 4e6 + 10; 5 6 int n, m; 7 int fa[N]; 8 9 int find(int x) { 10 return fa[x] == x ? fa[x] : fa[x] = find(fa[x]); 11 } 12 13 int get(int x, int y) { 14 if (x == 1) return y; // 格子在上面的横边 15 else if (y == m) return m + x - 1; // 格子在右边的竖边 16 else if (x == n) return m + n + m - y - 1; // 格子在下面的横边 17 else return m + m + n - 1 + n - x - 1; // 格子在左边的竖边 18 } 19 20 int main() { 21 cin >> n >> m; 22 for (int i = 1; i <= 2 * (n + m) - 4; i++) { 23 fa[i] = i; 24 } 25 26 if (n > m) swap(n, m); 27 for (int i = 1; i <= m; i++) { 28 // 向左的方向 29 if (i <= n) { // 分界线左边 30 fa[find(get(1, i))] = find(get(i, 1)); 31 fa[find(get(n, i))] = find(get(n - i + 1, 1)); 32 } 33 else { // 分界线右边 34 fa[find(get(1, i))] = find(get(n, i - n + 1)); 35 fa[find(get(n, i))] = find(get(1, i - n + 1)); 36 } 37 // 向右的方向 38 if (m - i + 1 <= n) { // 分界线右边 39 fa[find(get(1, i))] = find(get(m - i + 1, m)); 40 fa[find(get(n, i))] = find(get(n - m + i, m)); 41 } 42 else { // 分界线左边 43 fa[find(get(1, i))] = find(get(n, i + n - 1)); 44 fa[find(get(n, i))] = find(get(1, i + n - 1)); 45 } 46 } 47 48 int ret = 0; 49 for (int i = 1; i <= 2 * (n + m) - 4; i++) { 50 if (fa[i] == i) ret++; 51 } 52 cout << ret; 53 54 return 0; 55 }
这里还有一种数学解法,答案就是 gcd(n – 1, m – 1) + 1 ,具体证明就更加复杂了,这个当作结论来记好了。可以参考下面链接:
Solutions for Codeforces Beta Round #68: https://codeforces.com/blog/entry/1731
参考资料
AcWing 4718. 摆放棋子(AcWing杯 – 周赛):https://www.acwing.com/video/4530/
原文地址:http://www.cnblogs.com/onlyblues/p/16886845.html
