不平等博弈问题
今天打了2022ICPC合肥的热身赛,赛场上莫名其貌过了个B,本来队友们讨论半天,死活讨论不明白,然后就寻思怎么样也要交一发,然后就过了,,,过的莫名其貌的,于是来搜搜题解,没想到搜出来一个大知识点…
从一个问题入手……
其实就是热身赛的问题的简化版,下方的棋子,W代表白色,B代表黑色,Alice只能拿白色棋子,Bob只能拿黑色棋子,拿走一个棋子会把这个棋子右边的所有棋子全拿走,轮到谁没有可以操作的空间他就输了。
WBWWB
BBBWW
WBBWB
BBWWB
WBWBW
经过观察,可以发现,其实在一行里,最左边的棋子是谁的,那么这一行就是谁 “占有优势” 的,比如第二行,Alice再怎么拿也只能拿走最后的两个W,剩下的3个B可以让Bob慢慢操作三轮,在这三轮里Alice肯定会被迫消耗自己的棋子,这样看起来Bob就可以最少拿到 “比Bob多3个轮次的操作优势”
那么我们该怎么样量化的定义这个问题呢?
首先我们可以进行一个符合常识的假设:我们以轮次来进行衡量,每一个W设定一个+1,每一个B设定一个-1
那么对于如下情况:
BB
WWWW
就可以用这种方式轻松地算出来,4-2=2>0,看起来Alice可以操作的轮次足足比Bob多出来两轮,那么无论先手后手,都是Alice必胜
再考虑接下来的情况:
BB
WW
此时的特征值为 2-2=0,所以此时没有一个谁必胜的状态,这样也符合我们的模拟,此时谁先手就会把自己的轮次-1,双方轮次都是2,所以此时的状态是后手必胜的,不管Alice或是Bob。
但是这种特征值的设定方式真的正确吗? 我们考虑接下来这种情况:
WB
我们通过模拟可以发现:不管谁先手,都是Alice必胜,这也符合我们刚刚在最初提出问题时候的五行棋子所提到的假设:在单行里,最左边的棋子是谁的,那么在这一行里的赢家一定是谁
但是此时就不满足我们所设定的特征值的性质了!
所以我们需要设定一种新的特征值的衡量标准!
这种“特征值的衡量标准”需要满足:
-
对于 “WB” 这样的,特征值应该是一个正数,因为此状态是Alice必胜
-
“WB”的特征值也应该比1更小,或者说,与单个的“W“特征值不同,因为在下图的这种情况下,因为在第一行棋子是”WB“而不是”W“,所以给了Bob一丝喘息的机会,这使得让Bob先手的情况下,可以取第一行后面的B,让他可以获得胜利。
WB
B
所以我们根据以上的两个性质,我们可以大胆提出一个假设:
我们是否可以把”WB“的特征值设定为1/2呢?
为了验证上述假设,我们考虑接下来这两种情况:
WB
BW
WB
WB
B
对于第一个情况,可以经过验证,是后手必胜的状态,(当然这也是热身赛的题的样例)
对于第二个情况,可以发现,
-
如果Alice先手,那么其实只有一种走法,而之后的棋局就回到了我们刚刚举得例子里,所以Bob必胜(Bob取得某个在”W“后面的”B“)
-
如果Bob先手
- 如果Bob先拿了单独的B,那么显然Bob必输,因为我们已经知道剩下的两行都是”Alice占据先机“的行
-
如果Bob拿走了某个W后面的B,那么Alice只需要拿走一组完整的”WB“就好了,接下来Bob唯一的选择是选择单独的B,而Alice可以拿走”在第一轮中被Bob拿走了一个B“的那个W,接下来Bob无法操作,所以Alice获胜
综上,第二个情况是一个后手必胜的策略,而如果我们把单独的B的特征值定为-1,那么显然WB这样的特征值就是1/2。同理,BW这样的特征值就是 -1/2
注意,我们此时对于特征值的”加减“,已经没有了最初的对于轮次的求和那样的实际意义,也就是说此时我们是凭借直觉对于特征值进行加减,但是从结果来看,似乎这样的运算律是符合规律的
所以!一个问题就这样摆在我们面前,我们需要证明,我们对于棋局的特征值的赋予,是和数字具有相同的代数结构的,至少需要证明它可以进行加减运算,同时还要存在大小关系的比较
更进一步地,我们可以建立一个全体棋盘到全体实数的映射
超实数的提出
首先,是超实数的定义
我们要找到一种有序域,比实数域更大(不是复数域,因为复数域并不有序)
-
定义x={XL|XR},XL,XR表示两个数集
要求XL中任取一个元素都不大于x,且x不大于XR中任取的一个元素
-
定义偏序关系<=,对于x={XL|XR},y={YL|YR},x<=y等价于”XL中任取一个元素都不大于y,并且x不大于YR中任取的一个元素“
可以从定义1中证明出这组等价关系,而不是<=的递推性,此时需要使用数学归纳法来证明,而不是所谓的小于等于的传递关系,因为在这里的<=只是一个符号,并没有在我们的实数域下的数学意义
-
定义达利函数(x为实数,δ(x)为对应的超实数),为实数到超实数的映射
\(\LARGE \delta (x)=\left\{\begin{matrix} \{\; | \;\} , x=0 \\ \{x-1\; | \;\; \},x>0\wedge x \in Z \\ \{\;\;|\;x+1\},x<0\wedge x \in Z \\ \{\frac{j-1}{2^k} \;| \;\frac{j+1}{2^k}\},x=\frac{j}{2^k}\wedge j,k \in Z\wedge k>0 \end{matrix}\right.\)
- 注意,并不是每一个超实数都可以在达利函数中取到,但是这些超实数是可以计算的
比如{1/3 | 11/4}=1
- 同样的,达利函数的计算也不是十分准确的,接下来会给出最准确的计算方式
- 然后对于多元数集,x={XL|XR}={lmax|rmin}就可以计算出来了
-
定义达利函数的反函数,记作SN函数
\(\LARGE SN(x)=\left\{\begin{matrix} 0,x=\{\; | \;\}\ \\ max(0,l+1),x=\{l\;|\;\;\} , l\in Z \\ min(0,r-1),x= \{\;\;|\;r\} ,r\in Z \\ \frac{l+r}{2} ,x=\{l\;|\;r\} , r-l<=1 ,log(r-l)\in Z\end{matrix}\right.\)
- 其实这个反函数也少了一些情况,但是在简单的计算中是可以直接使用的,如果涉及到复杂计算,需要参考下面给出的最准确的计算方式
将左空集视作 -inf ,右空集视作 inf,然后用以下方法计算
① l < 0 且 r > 0,SN(x) = 0
② l , r 中间有整数
a. 0 <= l < r,SN(x) = floor ( l+1 )
b. l < r <= 0,SN(x) = ceil ( r-1 )
③ l , r 中间无整数,优先 k 最小,其次 j 最小,使得 l < j / 2^k < r
实际操作的时候往往是三点对应,一个局势(状态) 对应 一个实数 对应 一个超实数
在代码里,我们一般会把自变量写成状态,然后用其对应的超实数 计算 其对应的实数作为因变量
④加法:
x + y = {XL + y , x + YL | XR + y , x + YR }
⑤相反数:
-x = { -XR | -XL }
-0 = 0
a-b = a + (-b)
⑥超实数加法满足交换律和结合律
⑦与不平等博弈的关系:
a. 玩家L 操作的后继状态的SN值集合 XL,玩家R 操作的后继状态的SN值集合 XR
这个游戏可用超实数 x = { XL | XR } 表示
b.因为超实数域是有序域,所以多游戏的SN等于单个游戏的SN函数之和
c. x>0,L必胜 ; x<0,R必胜 ; x=0,后手必胜(一定注意是后手必胜,千万别记反了)
结合例题
例一:HDU-3544
有N个巧克力,长xi,高yi,Alice可以竖切,Bob可以横切,必须切整数,谁不能切谁就输了,Alice先手,问输赢
我们假设一个巧克力为一个游戏,那么对于一个长为1,高为1的巧克力,此时是空状态,双方都无法进行操作,即
SN(1,1)={ | }=0
SN(2,1) = {SN(1,1)+SN(1,1) | } = {0| } = 1
SN(3,1) = {SN{1,1}+SN(2,1) | } = {1| } = 2
SN(4,1) = {SN(1,1) + SN(3,1) , SN(2,1) + SN(2,1) | } =3
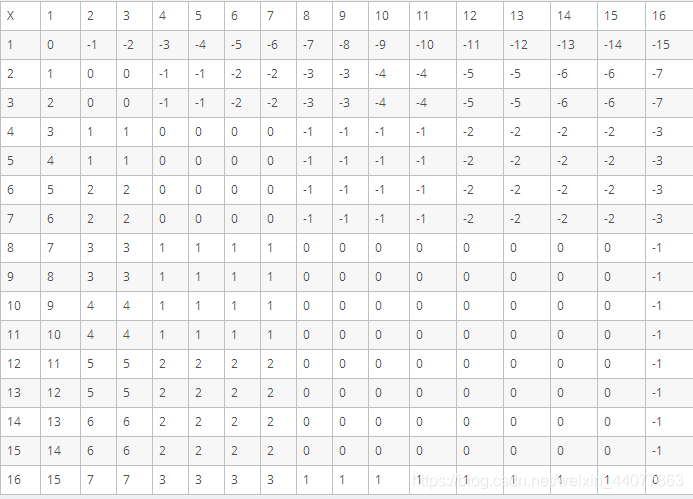
接下来我们打一个表找规律:
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
double sn[20][20];
double get_sn(int x,int y){
if(sn[x][y]!=inf) return sn[x][y];
double l=-inf,r=inf;
for(int i=1;i<=x/2;i++) l=max(l,get_sn(i,y)+get_sn(x-i,y));
for(int i=1;i<=y/2;i++) r=min(r,get_sn(x,i)+get_sn(x,y-i));
if(l<0&&r>0) sn[x][y]=0;
else if(floor(l+1)>l&&floor(l+1)<r){
if(l>=0) sn[x][y]=floor(l+1);
else sn[x][y]=ceil(r-1);
}
else{
int j,k,tmp=1;
bool ok=0;
for(k=1;!ok;k++){
tmp<<=1;
for(j=floor(l*tmp+1);!ok&&j<tmp*r;j++) if(j>l*tmp&&j<r*tmp){
ok=1;
break;
}
}
sn[x][y]=1.0*j/tmp;
}
return sn[x][y];
}
int main(){
for(int i=1;i<=16;i++) for(int j=1;j<=16;j++) sn[i][j]=inf;
for(int i=1;i<=16;i++) for(int j=1;j<=16;j++) printf("%.0f%c",get_sn(i,j),j==16?'\n':' ');
return 0;
}
-
可以发现是有规律的,即
$\LARGE SN(x,y) =\LARGE \frac{x}{2^{\lfloor logy \rfloor}} $
-
所以我们可以直接求出SN函数,接下来如果SN>0,那么Alice赢,否则Bob无论是作为后手还是必胜,都是Bob赢
-
AC代码:
#include<bits/stdc++.h> #define re register #define ll long long #define inc(i,j,k) for(re int i=j;i<=k;i++) #define dec(i,j,k) for(re int i=j;i>=k;i--) using namespace std; inline int read(){ re int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') {if(ch=='-') f=-1; ch=getchar();} while(ch>='0'&&ch<='9') {x=x*10+(ch^48); ch=getchar();} return x*f; } int T; int n; ll xx,yy; int main(){ T=read(); inc(zzt,1,T){ n=read(); ll sn = 0; inc(i,1,n){ cin>>xx>>yy; ll k=1; if(xx<yy) { swap(xx,yy); k=-1; } sn += k*(xx/ (ll)pow(2,(ll)log2(yy)) -1); } if(sn>0) printf("Case %d: Alice\n",zzt); else printf("Case %d: Bob\n",zzt); } }
例二: POJ 2931
t组数据,C1和C2两套塔,每套塔有三个塔,分别n1,n2,n3块砖,从上到下描述,有黑砖和白砖,白玩家可以拿走一个白砖及其上面的所有砖,一个黑玩家可以拿走一个黑砖及其上面的所有砖,白玩家为L玩家,黑玩家为B玩家,问 SN(C1) 是否 >=SN(C2)
首先,如果我们想到定义二位状态,以白子数和黑子数作为一个二位状态来定义一组游戏,但是似乎存在白子和黑子的顺序问题
-
当没有白子和黑子是
SN(无黑无白) = { | } = 0
-
我们考虑只有1个白子的情况:
W = SN(1白0黑) = {0| } = 1
- 只有1个黑子的情况:
B = SN(1黑0白) = { |0} = -1
- 只有x个白子的情况:
WW…WW = SN(x白0黑) = { SN(0), SN(1),SN(2),…,SN(x-1) | } = { 0,1,2,…,x-1 | } = x
- 只有y个黑子的情况:
BB…BB = SN(y黑0白) = -y
- 在x个白子后接1个黑子的情况:
WWWWWWB = SN(x白1黑) = { 前面还有好多,SN(x-1白0黑) | SN(x白0黑) } = { SN(x-1白0黑) | x } = {x-1 | x} = x-1/2
- 在x个白子后接2个黑子的情况:
WWWWWWBB = SN( <x,0> | <x+1,0> ) = {x-1 | x-1/2} = x-1/2-1/4
-
规律以及非常明显了:
前x个白子/黑子直接+x/-x,后面的从cnt=1开始,+/- 2^(-cnt)
-
如果怕精度出问题,可以直接通分,但是其实对于这道题根本不需要通分!因为根据计组,这样的二进制并没有被近似处理!
原文地址:http://www.cnblogs.com/ZzTzZ/p/16907421.html
