估计退化函数
图像观察估计
首先观察图像的一个小矩形区域,之后处理子图像得到想要的结果,得到一个子图像的原图像估计之后通过下式:
\[H_s(u,v) = \frac{G_s(u,v)}{\hat{F}_s(u,v)} \]
即可计算退化函数,之后基于位置不变的假设还原出完整的退化函数
试验估计
假如使用获取退化图像的设备类似的装置对一个冲激(小亮点来模拟)成像,得到退化的冲激响应,因为冲激的傅里叶变换为一个常量,所以可以得到:
\[H(u,v) = \frac{G(u,v)}{A} \]
其中\(A\)是一个描述冲激强度的常量
建模估计
对图像退化的过程进行数学建模
逆滤波
在知道退化函数的情况下复原图像的原始手段:
\[\hat{F}(u,v) = \frac{G(u,v)}{H(u,v)} = F(u,v) + \frac{N(u,v)}{H(u,v)} \]
可以看到,即使我们已经知道了退化函数,也不能准确的复原出原图像,因为\(N(u,v)\)是未知的,而且在退化函数的值是非常小的值的时候,\(\frac{N(u,v)}{H(u,v)}\)的值会支配原图像的估计值,我们可以通过限制滤波频率的方法来解决这个问题,我们可以将\(H(u,v)\)限制在原点附近,因为\(H(0,0)\)通常是\(H(u,v)\)的最高值
最小均方误差(维纳)滤波
该方法建立在图像和噪声都是随机变量的基础上,目标是找到未污染的图像\(f\)的一个估计\(\hat{f}\),使他们之间的均方误差最小:
\[e^2 = E\{(f – \hat{f})^2\} \]
现在假设噪声和图像不相关,且其中一个或者另一个有零均值,有下式:
\[\hat{F}(u,v) = \left[\frac{1}{H(u,v)}\frac{|H(u,v)|^2}{|H(u,v)|^2 + S_\eta(u,v)/S_f(u,v)}\right]G(u,v) \]
方括号中的项称为最小均方误差滤波器或最小二乘误差滤波器,式中\(H(u,v)\)是退化函数,\(S_\eta(u,v) = |N(u,v)|^2\)是噪声的功率谱,\(S_f(u,v) = |F(u,v)|^2\)是未退化图像的功率谱
许多有用的度量是以噪声和未退化的图像的功率谱为基础的,信噪比在频率域用下式近似:
\[SNR = \frac{\sum_{u = 0}^{M – 1}\sum_{v = 0}^{N – 1}|F(u,v)|^2}{\sum_{u = 0}^{M – 1}\sum_{v = 0}^{N – 1}|N(u,v)|^2} \]
均方误差可以描述成下式:
\[MSE = \frac{1}{MN}\sum_{u = 0}^{M – 1}\sum_{v = 0}^{N – 1}[f(x,y) – \hat{f}(x,y)]^2 \]
将复原图像考虑为信号,复原图像和原图像的差考虑为噪声,那么信噪比可以定义为:
\[SNR = \frac{\sum_{u = 0}^{M – 1}\sum_{v = 0}^{N – 1}\hat{f}(x,y)^2}{\sum_{u = 0}^{M – 1}\sum_{v = 0}^{N – 1}[f(x,y) – \hat{f}(x,y)]^2} \]
上式称为均方根信噪比或均方根误差,这个值和图像质量没有必然关系,因为未退化的功率谱大多数情况下是未知的,所以通常滤波器用下式来近似,其中\(K\)是一个常量:
\[\hat{F}(u,v) = \left[\frac{1}{H(u,v)}\frac{|H(u,v)|^2}{|H(u,v)|^2 + K}\right]G(u,v) \]
约束最小二乘方滤波
表达式如下:
\[\hat{F}(u,v) = \left[\frac{H^*(u,v)}{|H(u,v)|^2 + \gamma|P(u,v)|^2}\right]G(u,v) \]
其中\(\gamma\)是一个参数,需要计算p226,\(P(u,v)\)是
\[p(x,y) = \left[ \begin{matrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{matrix} \right] \]
的傅里叶变换
几何均值滤波器
\(\alpha,\beta\)是正的实常数,表达式为:
\[\hat{F}(u,v) = \left[\frac{H^*(u,v)}{|H(u,v)|^2}\right]^{\alpha} \left[\frac{H^*(u,v)}{|H(u,v)|^2 + \beta\left[\frac{S_\eta(u,v)}{S_f(u,v)}\right]}\right]^{1-\alpha}G(u,v) \]
由投影重建图像
X射线计算机断层重建图像中投影重建示意图:

如图可以看到关于物体的一个切片的生成,首先射线源发出射线穿过物体,被物体之后的检测器接受产生信号,这个信号因为物体和背景的吸收率不同而不同,这个信号经过反投影之后得到b中的条带,多个不同方向的射线反投影之后的条带叠加就可以得到物体的形状如图f,堆积这些切片就可以得到物体的三维体
涉及的数学知识
在笛卡尔坐标系中一条直线可以使用斜截式来表示\(y = ax + b\),或可由其法线表示来描述:
\[x\cos\theta + y\sin\theta = \rho \]
其中\(\rho\)是原点到直线的距离,\(\theta\)是\(x\)轴和直线法线的夹角,平行射线束的投影可由一组直线建模,如下图:
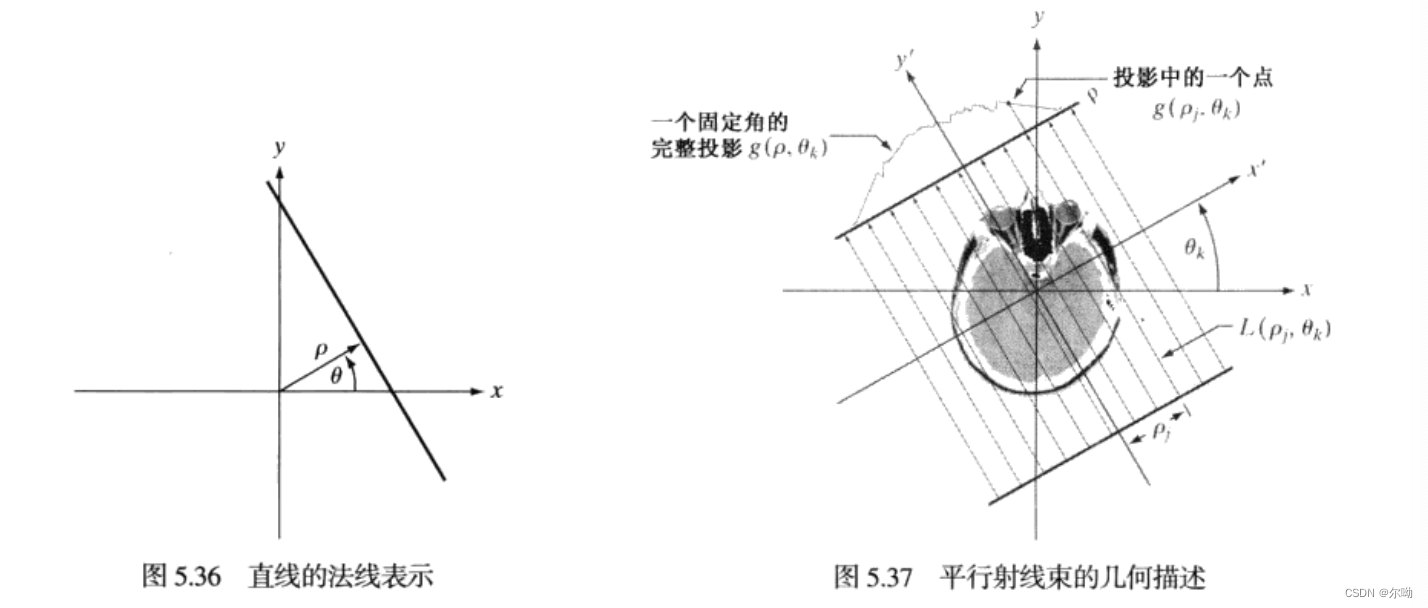
投射信号中的任意一点由沿着直线\(x\cos\theta_k + y\sin\theta_k = \rho_j\)的射线和给出:
\[g(\rho_j,\theta_k) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\delta(x\cos\theta_k + y\sin\theta_k – \rho_j)dxdy \]
上式使用了冲激函数\(\delta\)的性质,除非\(\delta\)的参量是0,否则上式的右边就是0,它指出积分只沿着线\(x\cos\theta_k + y\sin\theta_k = \rho_j\)计算,考虑\(\rho,\theta\)的所有值:
\[g(\rho,\theta) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\delta(x\cos\theta + y\sin\theta – \rho)dxdy \]
符号\(\mathcal{R}\{f(x,y)\}\)或\(\mathcal{R}\{f\}\)代替上式中的\(g(\rho,\theta)\)表示\(f\)的雷登变换,这个变换是投影重建的基石,给出了沿着\(xy\)平面中任意一条线的\(f(x,y)\)的投影(线积分)的公式,上式在离散情况下变为:
\[g(\rho,\theta) = \sum_{x = 0}^{M – 1}\sum_{y = 0}^{N – 1}f(x,y)\delta(x\cos\theta + y\sin\theta – \rho) \]
上面的公式中的\(f(x,y)\)在实际应用中指的是要重建的物体,例如CT扫描中的肿瘤,在不断旋转放射源的过程中得到不同的\(g(\rho,\theta)\),当雷登变换\(g(\rho,\theta)\)以\(\rho,\theta\)为横纵坐标轴,形成的图像为正弦图,该图像素和该像素处的\(g\)值成正比,正弦图包含重建\(f(x,y)\)所需的数据
CT的关键目的是从投影得到物体的三维表示,方法是反投影每一个投影,之后对反投影求和产生一幅图像(切片),堆积所有结果图像产生三维物体的再现,对于固定的\(\theta_k得到\)
\[f_{\theta_k}(x,y) = g(\rho,\theta_k) = g(x\cos\theta_k + y\sin\theta_k,\theta_k) \]
一般的:
\[f_{\theta}(x,y) = g(x\cos\theta + y\sin\theta,\theta) \]
通过对所有的反投影图像积分,得到最终图像:
\[f(x,y) = \int_0^\pi f_\theta(x,y)d\theta \]
在离散情况下:
\[f(x,y) = \sum_{\theta = 0}^\pi f_\theta(x,y) \]
傅里叶切片定理
关于\(\rho\)投影的一维傅里叶变换为:
\[G(\omega,\theta) = \int_{-\infty}^\infty g(\rho,\theta)e^{-j2\pi\omega\rho}d\rho \]
其中\(\omega\)是频率变量,\(\theta\)是给定的:
\[\begin{aligned} G(\omega,\theta) &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\delta(x\cos\theta + y\sin\theta – \rho)e^{-j2\pi\omega\rho}dxdyd\rho \\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\left[\int_{-\infty}^{\infty}\delta(x\cos\theta + y\sin\theta – \rho)e^{-j2\pi\omega\rho}d\rho \right]dxdy \\ &= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\left[e^{-j2\pi\omega(x\cos\theta + y\sin\theta)}\right]dxdy \end{aligned} \]
令\(u = \omega\cos\theta,v = \omega\sin\theta\)可得:
\[G(\omega,\theta)\left[ \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)e^{-j2\pi(ux + vy)}dxdy\right]_{u = \omega\cos\theta,v = \omega\sin\theta} \]
也就是该表达式与指定\(u,v\)时的\(f(x,y)\)的二维傅里叶变换等价:
\[G(\omega,\theta) = [F(u,v)]_{u = \omega\cos\theta,v = \omega\sin\theta} = F(\omega\cos\theta,\omega\sin\theta) \]
也就是一个投影的傅里叶变换可以通过得到投影区域的二维傅里叶变换的一个切片得到,如下图,右图是投影区域的傅里叶变换,那么指定\(\theta\)的投影就是沿着角度取一条线:
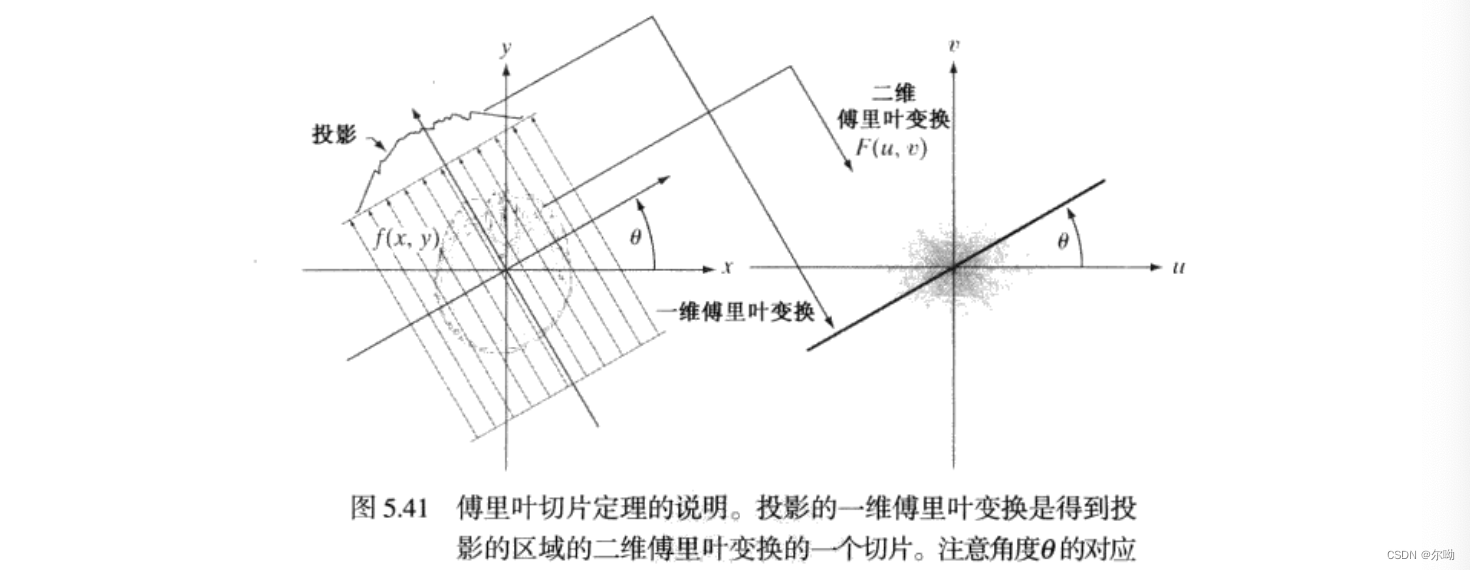
原文地址:http://www.cnblogs.com/eryoyo/p/16784141.html
1. 本站所有资源来源于用户上传和网络,如有侵权请邮件联系站长!
2. 分享目的仅供大家学习和交流,请务用于商业用途!
3. 如果你也有好源码或者教程,可以到用户中心发布,分享有积分奖励和额外收入!
4. 本站提供的源码、模板、插件等等其他资源,都不包含技术服务请大家谅解!
5. 如有链接无法下载、失效或广告,请联系管理员处理!
6. 本站资源售价只是赞助,收取费用仅维持本站的日常运营所需!
7. 如遇到加密压缩包,默认解压密码为"gltf",如遇到无法解压的请联系管理员!
8. 因为资源和程序源码均为可复制品,所以不支持任何理由的退款兑现,请斟酌后支付下载
声明:如果标题没有注明"已测试"或者"测试可用"等字样的资源源码均未经过站长测试.特别注意没有标注的源码不保证任何可用性



