题意简述
有\(n(0 \leq n \leq 5 \times 10^5)\)个单词与一常数\(m(0 \leq m \leq 10 ^ 3)\),第\(i\)个单词有一属性\(C_i\)(原题未给出\(C_i\)的取值范围,但应为正整数或非负整数),需要将所有这些单词按顺序分为任意组,若将第\(a\)至\(b\)个单词分为一组,则花费为\((\sum^b_{i = a}C_i)^2 + m\),求出最少花费。有多组数据,以EOF结束输入。
思路
斜率优化板子题。设\(f_i\)为将前\(i\)个单词分组后的最小花费,\(s_i\)为\(\sum^i_{k = 1}C_k\)(即\(C\)的前缀和),可写出状态转移方程为\(f_i = \min(f_j + (s_i – s_j)^2 + m)(0 \leq j < i)\),\(f_n\)即为最优解。若对于每一个\(i\),暴力枚举\(j\),时间复杂度是\(O(n^2)\),显然无法通过本题。
优化
将方程移项,得\(f_i – s_i^2 – m = \min(f_j + s_j^2 – 2s_is_j)(0 \leq j < i)\)。作如下代换:
- \(y_j = f_j + s_j^2\)
- \(k_i = 2s_i\)
- \(x_j = s_j\)
- \(b_i = f_i – s_i^2 – m\)
得\(b_i = \min(y_j – k_ix_j)\),恰好化为了直线方程的斜截式形式,且对于每个\(x_j, y_j\),都能够将其转换为平面直角坐标系上的一点\((x_j, y_j)\)。于是,此时的任务变为已知直线的斜率\(k_i\),需寻找一点\((x_j, y_j)\)使得该直线过该点的截距\(b_i\)最小。
注意到\(C_i \geq 0\),可知\(s_i\)单调递增,则\(k_i\)同样单调递增。我们可以将斜率为\(k_i\)的直线从下往上移,该直线碰到的第一个点\((x_j, y_j)\)即为使得截距\(b_i\)最小的点,此时\(f_i = f_j + (s_i – s_j)^2 + m\),即为此时的最优解。如图:
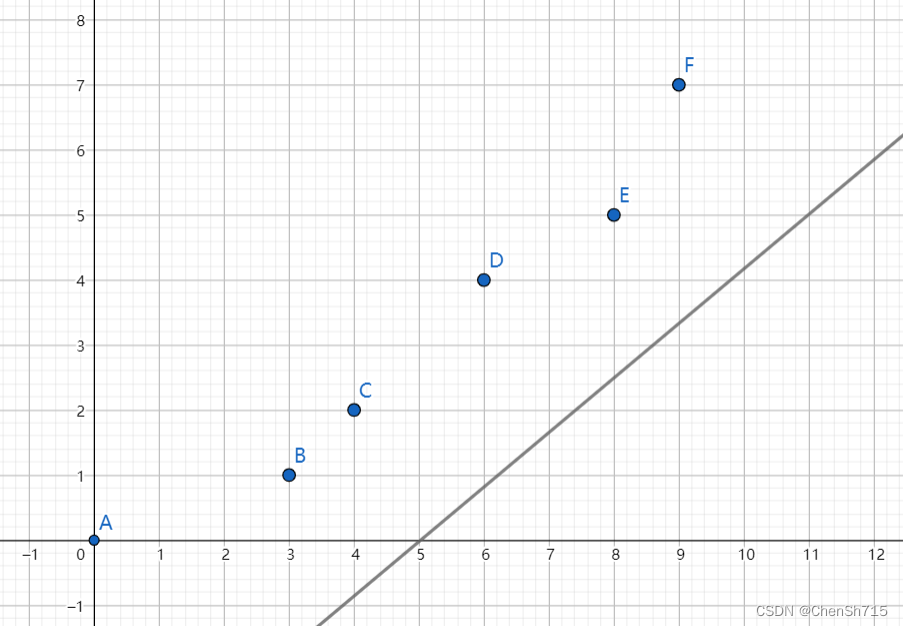
此时该直线由下往上运动碰到的第一个点即为所求。易知该直线碰到的第一个点一定是这些点所组成的下凸壳的顶点,如图:
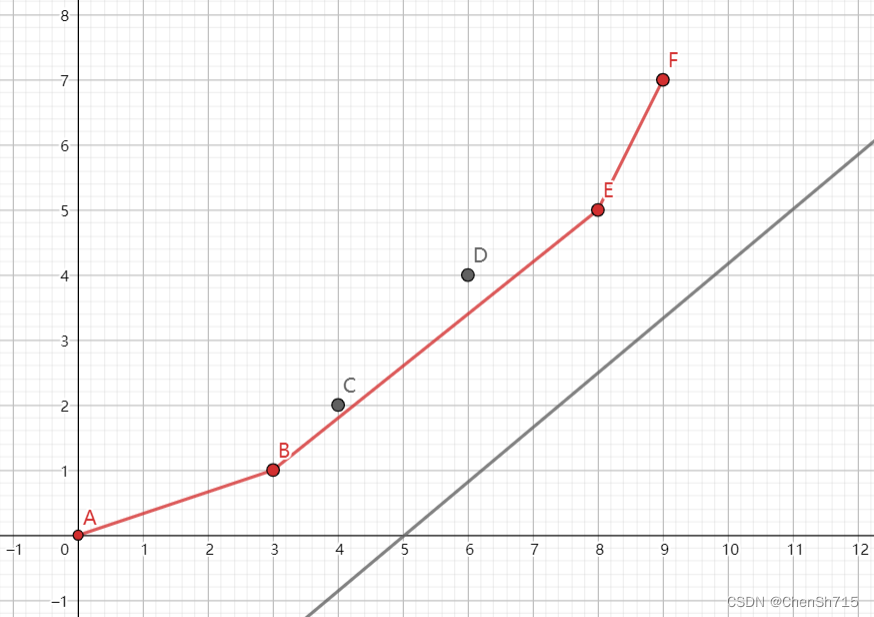
所以我们只需要维护之前所有的点所组成的下凸壳,每次判断直线与凸壳相交的顶点即可,可以使用单调队列维护每个点的编号。由于\(k_i\)单调递增,所以这次碰到的点一定是上次碰到的点或者其右边的点。判断碰到的点可以通过比较一个顶点相邻两条边的斜率和直线的斜率,设\(\mathop{\mathrm{slope}}(i, j)\)为编号为\(i, j\)的两点的斜率(非横坐标为\(i, j\)!),\(q_i\)为队列中第i个元素,若\(\mathop{\mathrm{slope}}(q_{j – 1}, q_j) \leq k_i < \mathop{\mathrm{slope}}(q_j, q_{j + 1})\),则\(q_i\)即为所求点的编号。由于下次的点编号一定大于等于这次的点编号,所以可以定义一个变量表示这次在队列中的下标,下次直接判断递增即可。每次求完\(f_i\)之后需要更新此时的凸壳。总时间复杂度\(O(n)\)。
代码:
#include <cstdio>
#define y(g) (f[g] + sqr(x(g)))
#define x(g) (sum[g])
#define sqr(x) ((x) * (x))
using namespace std;
typedef long long ll;
int n, m, q[500005], s, e;
ll sum[500005], f[500005];
int main() {
while (~scanf("%d %d", &n, &m)) {
s = e = 1; //此处隐含q[1] = 0,表示第一个编号是0,对应将前i个单词全部分为一组的情况
for (int i = 1; i <= n; ++i) {
scanf("%lld", &sum[i]);
sum[i] += sum[i - 1];
while (s < e && y(q[s + 1]) - y(q[s]) <= 2 * x(i) * (x(q[s + 1]) - x(q[s]))) ++s;
f[i] = f[q[s]] + sqr(x(i) - x(q[s])) + m;
while (s < e && (y(q[e]) - y(q[e - 1])) * (x(i) - x(q[e])) >= (y(i) - y(q[e])) * (x(q[e]) - x(q[e - 1])))
--e;
q[++e] = i;
}
printf("%lld\n", f[n]);
}
return 0;
}
原文地址:http://www.cnblogs.com/wf715/p/hdu-3507-print-article.html
