斐波那契数列

https://blog.csdn.net/weixin_39922642/article/details/111103715

斐波那契数列(Fibonacci sequence)，又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n – 1)+F(n – 2)(n ≥ 3，n ∈ N*)在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用。

1、递归

1 public static long f1(int n, long[] f) {        if (n < 1) {            throw new RuntimeException("输入参数小于1");        }        if (n == 1 || n == 2) {            return 1;        }         if (f[n] == 0) {            f[n] = f1(n-1, f) + f1(n-2, f);        }        return f[n];    }

public static long f1(int n, long[] f) { if (n < 1) { throw new RuntimeException("输入参数小于1"); } if (n == 1 || n == 2) { return 1; } if (f[n] == 0) { f[n] = f1(n-1, f) + f1(n-2, f); } return f[n]; }

递归比较直观，但是由于是逆推，重复计算，所以效率低下，可加入map对象查找进行优化，但是由于递归的本质，会导致栈溢出风险，不推荐。

2、顺序加

public static long f2(int n) {        if (n <= 0) {            throw new RuntimeException("输入参数小于1");        }        if (n == 1 || n == 2) {            return 1;        }         long a = 1;        long b = 1;        long c = 0;         for (int i = 3; i <= n; i++) {            c = a + b;            a = b;            b = c;        }        return c;    }

public static long f2(int n) { if (n <= 0) { throw new RuntimeException("输入参数小于1"); } if (n == 1 || n == 2) { return 1; } long a = 1; long b = 1; long c = 0; for (int i = 3; i <= n; i++) { c = a + b; a = b; b = c; } return c; }

无递归栈溢出风险，效率高，时间复杂度O(n).

3、数学表达式计算

通过数学推导，可得出如下结论：

public static long f3(int n) {        double result = 0;        double temp = Math.sqrt(5.0);        result = (Math.pow((1 + temp) / 2, n) - Math.pow((1 - temp) / 2, n)) / temp;        return (long) result;    }

public static long f3(int n) { double result = 0; double temp = Math.sqrt(5.0); result = (Math.pow((1 + temp) / 2, n) - Math.pow((1 - temp) / 2, n)) / temp; return (long) result; }

时间复杂度依赖于java计算方式。但是由于计算机精度问题，导致该方式在n=71之后就不再准确。

4、矩阵快速幂

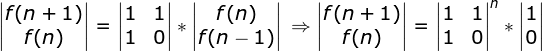
public static long f4(int n){        if (n <= 0) {            throw new RuntimeException("输入参数小于1");        }        if (n == 1 || n == 2) {            return 1;        }         //单位矩阵        long[][] result = {{1}, {0}};        long[][] tem = {{1, 1}, {1, 0}};         while (n != 0) {            if ((n & 1) == 1) {                result  = matrixMultiply(tem, result);            }            tem = matrixMultiply(tem, tem);            //右移一位并赋值            n >>= 1;        }        return  result[1][0];    }

public static long f4(int n){ if (n <= 0) { throw new RuntimeException("输入参数小于1"); } if (n == 1 || n == 2) { return 1; } //单位矩阵 long[][] result = {{1}, {0}}; long[][] tem = {{1, 1}, {1, 0}}; while (n != 0) { if ((n & 1) == 1) { result = matrixMultiply(tem, result); } tem = matrixMultiply(tem, tem); //右移一位并赋值 n >>= 1; } return result[1][0]; }

两个矩阵的乘法：(矩阵相乘方法：http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html)

/*矩阵乘法*/    private static long[][] matrixMultiply(long[][] a, long[][] b){        int rows = a.length;        int cols = b[0].length;        long[][] matrix = new long[rows][cols];        for (int i = 0; i < a.length; i++) {            for (int j = 0; j < b[0].length; j++) {                for (int k = 0; k < a[i].length; k++) {                    matrix[i][j] += a[i][k] * b[k][j];                }            }        }        return matrix;    }

/*矩阵乘法*/    private static long[][] matrixMultiply(long[][] a, long[][] b){ int rows = a.length; int cols = b[0].length; long[][] matrix = new long[rows][cols]; for (int i = 0; i < a.length; i++) { for (int j = 0; j < b[0].length; j++) { for (int k = 0; k < a[i].length; k++) { matrix[i][j] += a[i][k] * b[k][j]; } } } return matrix; }

虽然matrixMultiply方法中为for循环嵌套，但是由于斐波那契数列为2*2矩阵，其循环次数一定，时间复杂度可看为O(1),故矩阵快速幂方式求解斐波那契数列时间复杂度为O(logn)。

原文地址：http://www.cnblogs.com/wwkk/p/16798928.html