树与二叉树
1.n-1=Knk 结点数与度数的关系
2.满k树的编号为i的结点的双亲结点编号:j=⌊i-2/k⌋+1;结点i的最后一个孩子编号为(i-1)*k+1,当(i-1)%k != 0时,结点i有右兄弟,编号为i+1。
3.完全二叉树的最后一个非终端结点序号:⌊n/2⌋
4.二叉树前中后序中,左右孩子的相对顺序是一样的,所有叶子结点的访问次序是一样的。
5.二叉树转树:从结点的左孩子开始,一直向右走,这些结点即为结点的孩子们;二叉树转森林:根开始一路向右,断开所有的边。
6.树的后序遍历,访问顺序与其对应的二叉树中序遍历顺序相同;森林的后序遍历是各个树后序遍历的线性相加
7.哈夫曼树的构造:先对元素进行排序,后找最小的两个进行求和产生根,然后删除刚刚取出的两个最小元素并将根插入队列,接着再寻找两个最小的元素求和,如此往复。(按层排好)
树的路径长度PL:从根结点到每个结点的路径长度之和。(∑层数*每层的结点树,根结点是第0层)
树的带权路径长度WPL:树种所有叶子结点的带权路径长度之和。(∑层数*每层叶结点权值之和,根结点是第0层)
哈夫曼编码:从哈夫曼树根结点出发,左走0,右走1
8.二叉排序树构造:底部插入,且左子树L<根P<右子树R,故RPL形式的遍历得到从到大小的序列。
9.查找失败和查找成功:查找失败的分母是空结点的数量,查找成功的分母是实结点的数量。查找失败的分子是比较次数*各层空结点数,查找成功其式子中分子均为各层结点数*查找次数,根结点查找次数为1。
10.二叉树的删除结点:①叶子结点直接删除②只有一棵右子树或者一棵左子树,将其孩子放到现在自己的位置③既有左子树又有右子树,将结点的数据域用其直接前驱数据域覆盖,然后删除直接前驱;直接后继同理
二叉排序树中序遍历下的直接前驱和直接后继:
直接前驱(有的话):A的左孩子代表的树的最右侧的结点。
直接后继(有的话):A的右孩子代表的树的最左侧的那个结点
11.平衡二叉树:
LL: RR:取相反转 LR、RL:按从左到右顺序转
图
1.无向图的全部顶点的度之和等于边数的两倍;含有n个顶点的无向完全图有n(n-1)/2条边,最多边数:n个顶点的有向完全图有n(n-1)条有向边。
2.矩阵An的元素An[i][j]等于由顶点i到顶点j的长度为n的路径的数目。
无向图中矩阵中行(列)非零元素的个数就是该点的度
3.图的广度优先生成树就是二叉树的层序遍历:一链一层,一层访问完即回溯(队列)
4.邻接表占用空间较多,适合稀疏图;邻接矩阵与边数少,适合稠密图。
5.Prim和Kruskal最小生成树的方法。
单元最短路径:Dijkstra算法,即表格法按趟数每次最短(贪心 ),每次确定一个点
Flyord:即题目中会出现dist-1,dist0…..(即每一步的结果)。
此方法:①先将主对角线处元素对应顶点画十字,十字所在行列元素不变照抄
②十字区域内有∞的,则该位置的对应的行与列均不变照抄
③主对角线元素全为0,直接照抄
④剩余位置,从该位置做十字。与第①次的红十字相交的值,将两值相加,与原位置值相比,取最小者入原位置。
6.时间允许发生的最早时间和最晚时间:正找、相加,取max;反找、相减,取min。
7.在带权图中,没有边用0和∞表示都可以。
8.AOE网:①画出源点,所有没有先驱工序的边都由源点发出。②所有没有出现在先驱工序里的边都指向最后一个顶点——汇点。
工序是工序,顶点是顶点。工序在边上,顶点为Vi
查找
1.折半查找过程中带外部结点的判定树。
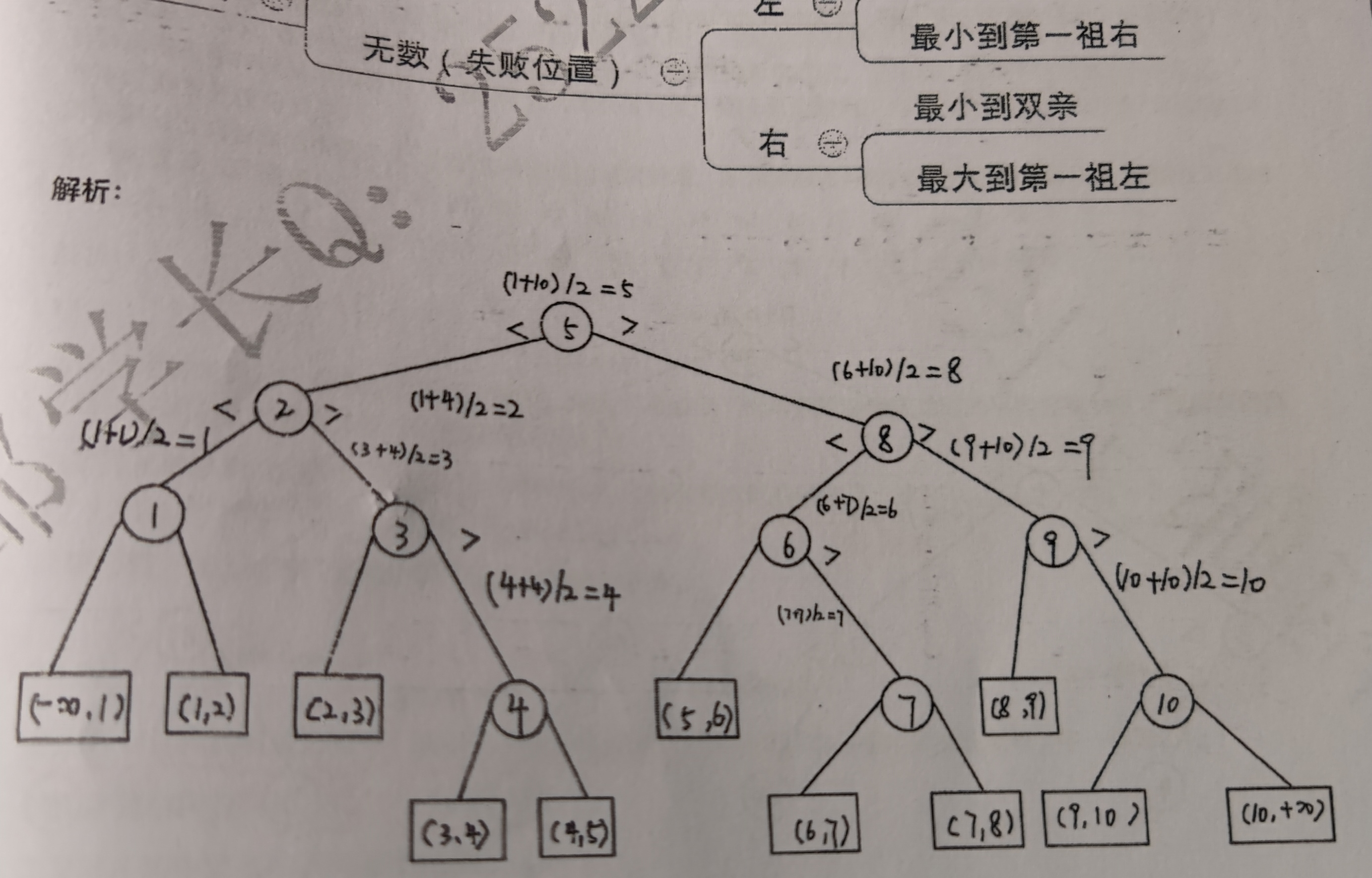
2.为了提高顺序查找的效率,将查找概率高的放在最先被查找的位置(先好后坏)
散列表
1.平均查找长度ASL:查找成功的分母是关键字数,如7;查找失败的分母是散列函数所能映射的地址数最大值。
查找失败的分子是从左边第一个元素开始,当它所遇到的第一个空位置,从该元素出发一共有几个数,依次处理后累加(0~P-1,P为%P的P)
H(key)=(key*3)%7
线性探测法即探测到空位置就停下来了。总共需要探测k(1+k)/2次探测。每次解决冲突均从H1(H0)开始
排序
1.二分法插入排序与记录初始状态无关
2直接插入排序:空间O(1),时间O(n^2)
void InsertSort(Element A[], int n)
{
int i, j;
for(i = 2;i <= n; i++){
if(A[i] < A[i-1])
A[0] = A[i];
for(j = i-1; A[j] > A[0]; --j)
A[j+1] = A[j];
A[j+1] = A[0];
}
}
2.3倍移动次数是冒泡排序的考法:比较次序=交换次序=n(n-1)/2,移动次序=3n(n-1)/2.
冒泡排序空间O(1),时间O(n^2)
3.稳定性:插冒归,统计基
4.快排的一些细节 在P135 第4题,请自行查看
5.得到一个序列中前k个最小元素的部分排列序列,首选堆排序。堆排序是顺序存储的,因为涉及到随机访问。
归并排序代码

原文地址:http://www.cnblogs.com/jjw-code/p/16852425.html
