SVM Summary
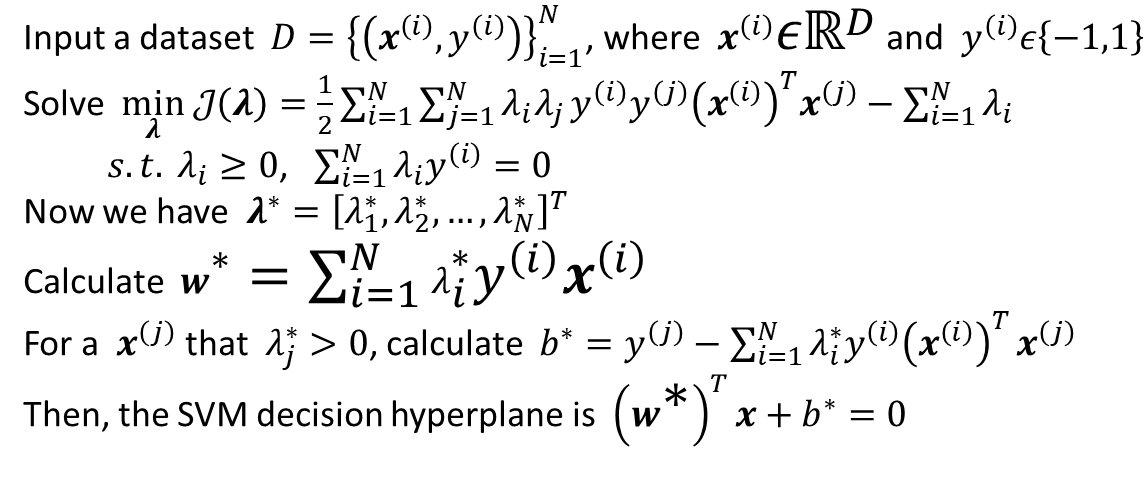
Example
Suppose the dataset contains two positive samples \(x^{(1)}=[1,1]^T\) and\(x^{(2)}=[2,2]^T\), and two negative samples \(x^{(3)}=[0,0]^T\) and \(x^{(4)}=[-1,0]^T\). Please calculate the SVM decision hyperplane.
Calculate
\[\min_\lambda\ {\mathcal{J}(\lambda)} = \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \lambda_i\lambda_jy^{(i)}y^{(j)}(x^{(i)})^Tx^{(j)} – \sum_{i=1}^N\lambda_i \]
\[s.t. \ \ \ \ \ \ \ \ \lambda_i \geqslant 0,\ \ \ \ \ \ \sum_{i=1}^N\lambda_iy^{(i)}=0 \]
由\(Dataset\ D:\{x:\{[1,1],[2,2],[0,0],[-1,0]\},y:\{1,1,-1,-1\}\}\)可得下式:
\[\min_\lambda\ {\mathcal{J}(\lambda)} = \frac{1}{2}(2\lambda_1^2+8\lambda_2^2+\lambda_4^2+8\lambda_1\lambda_2+2\lambda_1\lambda_4+4\lambda_2\lambda_4) \\- \lambda_1-\lambda_2-\lambda_3-\lambda_4\\ s.t \ \ \ \ \ \ \ \lambda_1 \geqslant 0,\lambda_2\geqslant 0,\lambda_3\geqslant 0,\lambda_4\geqslant 0\\ \lambda_1+\lambda_2-\lambda_3-\lambda_4 = 0 \]
since \(\lambda_1+\lambda_2 = \lambda_3+\lambda_4 \to \lambda_3 = \lambda_1+\lambda_2 – \lambda_4\):
\[\min_\lambda\ {\mathcal{J}(\lambda)} = \lambda_1^2+4\lambda_2^2+\frac{1}{2}\lambda_4^2+4\lambda_1\lambda_2+\lambda_1\lambda_4+2\lambda_2\lambda_4 – 2\lambda_1-2\lambda_2\\ s.t \ \ \ \ \ \ \ \lambda_1 \geqslant 0,\lambda_2\geqslant 0 \\ \\ \Longrightarrow ^{求偏导}\\ \left\{\begin{matrix} \frac{\partial \mathcal{J}}{\partial \lambda_1} = 2\lambda_1 +4\lambda_2+\lambda_4-2=0 \\ \frac{\partial \mathcal{J}}{\partial \lambda_2} = 4\lambda_1 +8\lambda_2+2\lambda_4-2=0 \\ \frac{\partial \mathcal{J}}{\partial \lambda_4} = \lambda_1 +2\lambda_2+\lambda_4=0 \end{matrix}\right. \]
Lagrange无解,所以极小值在边界上:
- 令\(\lambda_1 = 0, \lambda_3 = \lambda_1+\lambda_2 – \lambda_4\)带入\(\mathcal{J}(\lambda)\)中,得:
\[\mathcal{J}(\lambda) = 4\lambda_2^2+\frac{1}{2}\lambda_4^2++2\lambda_2\lambda_4 -2\lambda_2 \\ \\ \Longrightarrow ^{求偏导}\\ \left\{\begin{matrix} \frac{\partial \mathcal{J}}{\partial \lambda_2} = 8\lambda_2+2\lambda_4-2=0 \\ \frac{\partial \mathcal{J}}{\partial \lambda_4} = 2\lambda_2+\lambda_4=0 \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} \lambda_2=\frac{1}{2} \\ \lambda_4=-1(\le0 \ \ \ \ 不满足s.t.) \end{matrix}\right.\\ 再令:\\ \lambda_2 = 0,则\lambda_4=0, \mathcal{J}(\lambda) = 0;\\ 或\lambda_4 = 0,则\lambda_2=\frac{1}{4}, \mathcal{J}(\lambda) = -\frac{1}{4}; \]
同理可得:
- \(\lambda_2 = 0\)
\[\lambda_1 = 0,则\lambda_4=0, \mathcal{J}(\lambda) = 0;\\ 或\lambda_4 = 0,则\lambda_1=1, \mathcal{J}(\lambda) =-1; \]
- \(\lambda_3 = 0\)
\[\lambda_1 = 0,则\lambda_2=\frac{2}{13}, \mathcal{J}(\lambda) = -\frac{2}{13};\\ 或\lambda_2 = 0,则\lambda_1=\frac{2}{5}, \mathcal{J}(\lambda) =-\frac{2}{5}; \]
- \(\lambda_4 = 0\)
\[\lambda_1 = 0,则\lambda_2=\frac{1}{4}, \mathcal{J}(\lambda) = -\frac{1}{4};\\ 或\lambda_2 = 0,则\lambda_1=1, \mathcal{J}(\lambda) =-1; \]
综上:\(\lambda_{1,2,3,4} =\{1,0,1,0\}\)
\[ \left\{\begin{matrix} W=\sum_{i=1}^{N} \lambda_{i} y^{(i)} \boldsymbol{x}^{(i)}\\ b=y^{(j)}-\sum_{i=1}^{N} \lambda_{i} y^{(i)}\left(x^{(i)}\right)^{T} x^{(j)} \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} W = [1,1]^T\\ b=-1 \end{matrix}\right. \\\Longrightarrow x^{(1)}+x^{(2)} -1 =0 \]
原文地址:http://www.cnblogs.com/ACxz/p/16886274.html
1. 本站所有资源来源于用户上传和网络,如有侵权请邮件联系站长!
2. 分享目的仅供大家学习和交流,请务用于商业用途!
3. 如果你也有好源码或者教程,可以到用户中心发布,分享有积分奖励和额外收入!
4. 本站提供的源码、模板、插件等等其他资源,都不包含技术服务请大家谅解!
5. 如有链接无法下载、失效或广告,请联系管理员处理!
6. 本站资源售价只是赞助,收取费用仅维持本站的日常运营所需!
7. 如遇到加密压缩包,默认解压密码为"gltf",如遇到无法解压的请联系管理员!
8. 因为资源和程序源码均为可复制品,所以不支持任何理由的退款兑现,请斟酌后支付下载
声明:如果标题没有注明"已测试"或者"测试可用"等字样的资源源码均未经过站长测试.特别注意没有标注的源码不保证任何可用性
